[Algorithm] 위상 정렬(Topological Sort)을 위한 Kahn's Algorithm with JAVA

Algorithm/Graph

[Algorithm] 위상 정렬(Topological Sort)을 위한 Kahn's Algorithm with JAVA

jundyu 2025. 5. 23. 23:20

들어가며

제목에서 알 수 있듯이 이번 글은 위상 정렬을 위한 Kahn's 알고리즘에 대한 글입니다. 그래프와 관련된 알고리즘이므로 아래의 그래프 이론과 해당 글에 연계된 그래프 탐색 알고리즘 글들을 먼저 읽어보면 이해하기 쉽습니다.

[Algorithm] 그래프 이론 및 그래프 탐색

들어가며그래프는 제가 가장 좋아하는 알고리즘 분류입니다! 그래프 이론을 배우고 나면 단순한 자료 구조를 넘어서, 너비 우선 탐색, 깊이 우선 탐색, 최단 경로 탐색, 교착상태 판별 등 다양한

jundyu.tistory.com

위상 정렬 : Topological Sort

1. 개념

위상 정렬이란 유향 그래프의 정점들을 변의 방향을 거스르지 않도록 나열하는 것입니다. 사전적 의미로는 어려울 수 있는데, 쉽게 말하면 해야할 일의 순서를 정하는 것입니다.

위상 정렬은 주로 단방향 그래프에서 사용되며 각 정점들은 반드시 진입 차수 또는 진출 차수가 하나 이상 존재합니다. 이때 만약 A → B라면 A는 B보다 선행되어야하는 일입니다.

이렇게 선행 작업과 후속 작업 간의 순서를 정리해주는 것이 위상 정렬입니다.

아래는 이해를 돕기 위한 그림입니다.

위의 그래프를 기준으로 위상 정렬한 결과는 다음과 같습니다.

(1) → (4) → (2) → (3) → (5) → (6)

여기서 주의할 점은 1번과 4번 노드끼리는 선후 관계가 없으므로 순서가 바뀌어도 상관없습니다. 또한 2, 3, 5번 노드도 마찬가지로 선후 관계가 없으므로 세 노드끼리는 순서가 바뀌어도 상관없습니다.

2. 필요성

위상 정렬은 아래와 같은 상황에서 주로 사용됩니다.

수강 과목 순서
파일 컴파일 순서
작업 스케줄링

3. 특징

1. 단방향 그래프에 사이클이 존재하면 안 됨

사이클이 존재하면 일의 우선순위를 정할 수 없습니다. 위 그림을 보면 1번 작업을 위해 3번 작업을 먼저 수행해야하고, 3번 작업을 위해 2번 작업을 먼저 수행해야하는데 2번 작업을 위해선 1번 작업을 진행해야합니다.

이처럼 사이클이 존재하는 경우 교착 상태(Deadlock)에 빠지기 때문에 사이클이 없는 방향 비순환 그래프(DAG : Directed Acyclic Graph)에서만 위상 정렬을 사용할 수 있습니다.

교착 상태(Deadlock)란?

운영체제에서 발생하는 교착 상태란 여러 개의 프로세스가 서로 자원을 점유한 채, 상대 작업이 자원을 내놓기를 기다리면서 아무것도 진행되지 않는 상태를 말합니다.
위상 정렬에서도 마찬가지로 모든 작업이 다른 작업이 끝나길 기다리는 상태가 되어 아무것도 시작할 수 없는 교착 상태가 됩니다.

2. 위상 정렬은 대표적으로 Kahn's Algorithm과 DFS 방식이 있음

이번 글에선 칸의 알고리즘 방식을 채택하여 위상 정렬을 설명하겠습니다.

3. 위상 정렬의 결과는 하나가 아님

위의 그림에서 2, 3번 노드처럼 노드끼리 우선 순위가 존재하지 않는 경우에 위상 정렬의 결과는

1번 → 2번 → 3번 → 4번
1번 → 3번 → 2번 → 4번

으로 모두 가능합니다.

Kahn's Algorithm : 칸의 알고리즘

1. 개요

Kahn's 알고리즘은 1962년 Arthur B. Kahn이 최초로 발표한 대표적인 위상 정렬 알고리즘입니다. DFS 방식도 있지만 주로 Kahn의 알고리즘 방식을 많이 사용합니다.

2. 동작 방식

주어진 간선 정보를 전부 탐색하며 진입 차수 배열을 갱신
진입차수가 0인 노드를 전부 큐에 삽입
큐에서 노드 하나를 뽑아 해당 노드가 가리키는 모든 노드의 진입차수를 1씩 감소
만약 1만큼 줄인 진입차수가 0이 되었다면 큐에 삽입
큐가 빌 때까지 2~3을 반복

글로는 이해하기 어렵기 때문에 아래에서 그림과 함께 설명하겠습니다.

3. 특징

1. 시간 복잡도는 O(V + E)

칸 알고리즘은 처음 모든 간선을 확인하면서 정점의 진입 차수를 계산합니다. → E

그리고 모든 정점은 큐에 한번씩 들어가면서 확인합니다. → V

따라서 시간 복잡도는 O(V + E)가 됩니다.

2. BFS 방식

칸 알고리즘은 진입 차수가 0인 노드부터 차례대로 탐색하는 BFS 방식의 알고리즘입니다.

3. Queue 자료구조 사용

BFS 알고리즘이기 때문에 큐를 사용하여 인접한 노드부터 차례대로 확장해나갑니다.

4. 진입 차수를 저장할 1차원 배열 필요

각 정점으로 진입하기 위해 먼저 방문해야하는 정점이 몇개있는지 배열에 저장하기 위해서 배열이 필요합니다.

그림으로 이해하는 Kahn's Algorithm 동작

위의 그래프를 예시로 칸 알고리즘을 설명하겠습니다.

그래프는 인접 리스트 형태로 저장하고, 진입 차수는 int 타입의 1차원 배열로 저장합니다. 그리고 큐 자료구조를 사용합니다.

1. 각 노드별 진입 차수 저장

우선 1번부터 9번까지 각 노드에 진입 차수를 저장합니다.

그래프를 보면 알 수 있듯이 해당 노드로 진입하는 간선의 개수를 저장했습니다.

2. 진입 차수가 0인 노드 큐에 삽입

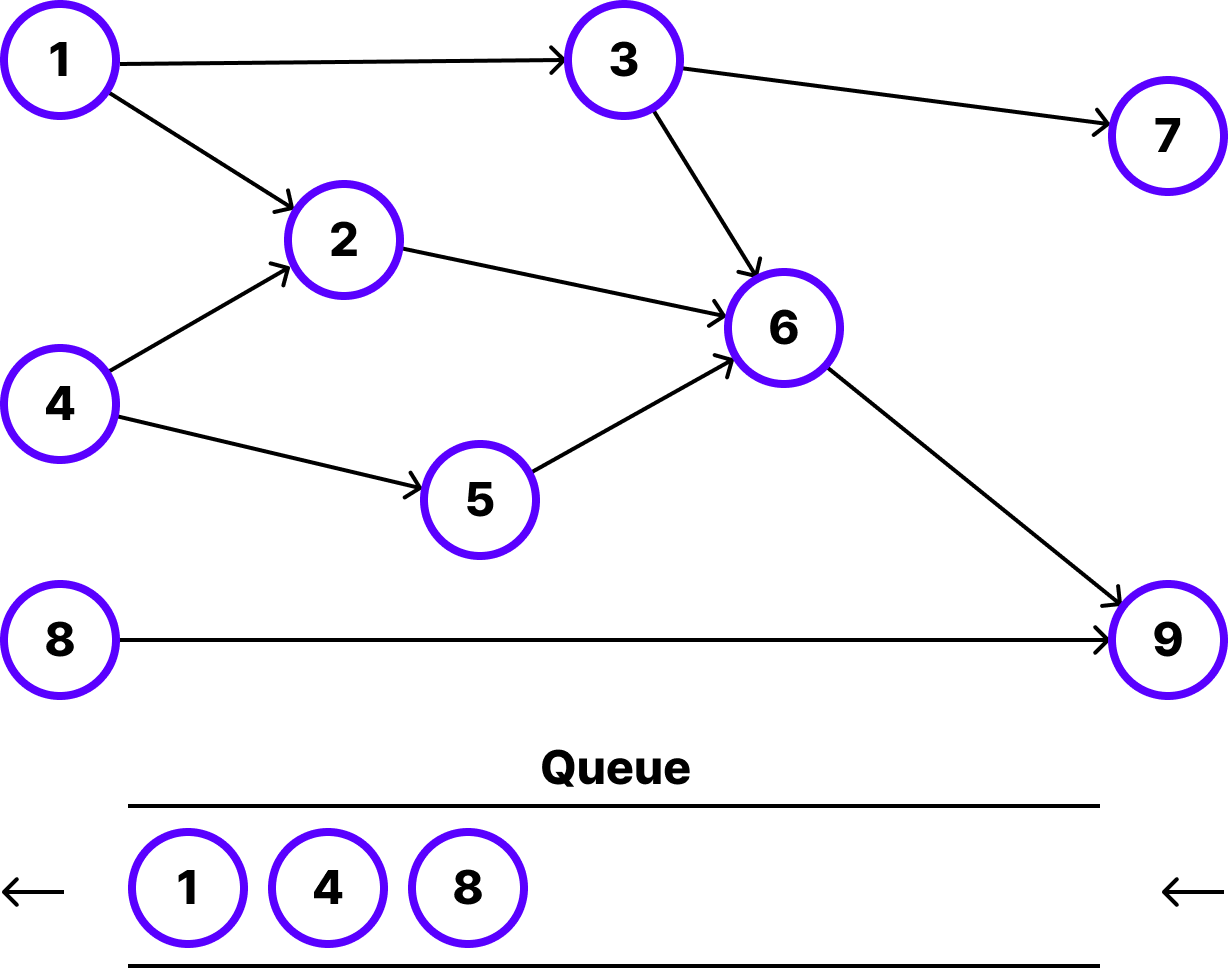
우선 최초에는 진입 차수 배열의 전체를 탐색하면서 큐에 진입 차수가 0인 노드들을 삽입합니다. 따라서 1, 4, 8번 노드를 큐에 삽입합니다. 큐에 진입 차수가 0인 노드를 삽입할 때 순서는 중요하지 않습니다.

진입 차수가 0인 노드를 추가하는 이유?

진입 차수가 0이라는 의미는 해당 노드로 접근하기 위해 먼저 접근해야하는 노드가 존재하지 않음을 의미합니다. 따라서 위상 정렬을 시작할 때는 진입 차수가 0인 노드들부터 우선적으로 처리하게 됩니다.

3. 1번 노드를 추출해서 인접한 노드들 진입 차수 감소

1번 노드를 추출해서 1번 노드와 인접한 2번 노드와 3번 노드의 진입 차수를 1씩 감소시킵니다. 2번 노드와 3번 노드에 접근하기 위해서 먼저 방문해야하는 노드를 하나 방문했다는 의미입니다.

진입 차수를 1 감소시켰는데 만약 0이 된다면 이제 해당 노드를 방문할 준비가 되었다는 뜻입니다. 따라서 진입 차수가 0인 3번 노드를 큐에 삽입합니다.

회색은 이미 방문한 노드와 방문했기 때문에 의미없는 간선을 뜻합니다.

4. 4번 노드를 추출해서 인접한 노드들 진입 차수 감소

4번 노드를 추출합니다. 4번 노드는 2번, 5번 노드와 인접했으므로 각각 진입 차수를 1씩 감소시킵니다.

진입 차수를 1 감소시켰더니 2번, 5번 노드 전부 진입 차수가 0이 되어서 큐에 삽입합니다. 즉, 2번 노드를 방문하기 위한 조건을 만족했다는 뜻이고, 5번 노드를 방문하기 위한 조건을 만족했다는 뜻입니다.

5. 8번 노드를 추출해서 인접한 노드들 진입 차수 감소

이제 반복되는 설명은 빠르게 넘어가겠습니다.

8번 노드와 인접한 9번 노드의 진입 차수를 1 줄이고, 9번 노드를 큐에 삽입합니다.

6. 3번 노드를 추출해서 인접한 노드들 진입 차수 감소

3번 노드를 추출하고 인접한 6, 7번 노드의 진입 차수를 1씩 감소시킵니다. 7번 노드의 진입 차수가 0이 됐으므로 큐에 추가합니다.

7. 2번 노드를 추출해서 인접한 노드들 진입 차수 감소

2번 노드를 추출하고 인접한 6번 노더의 진입 차수를 1만큼 감소시킵니다.

8. 5번 노드를 추출해서 인접한 노드들 진입 차수 감소

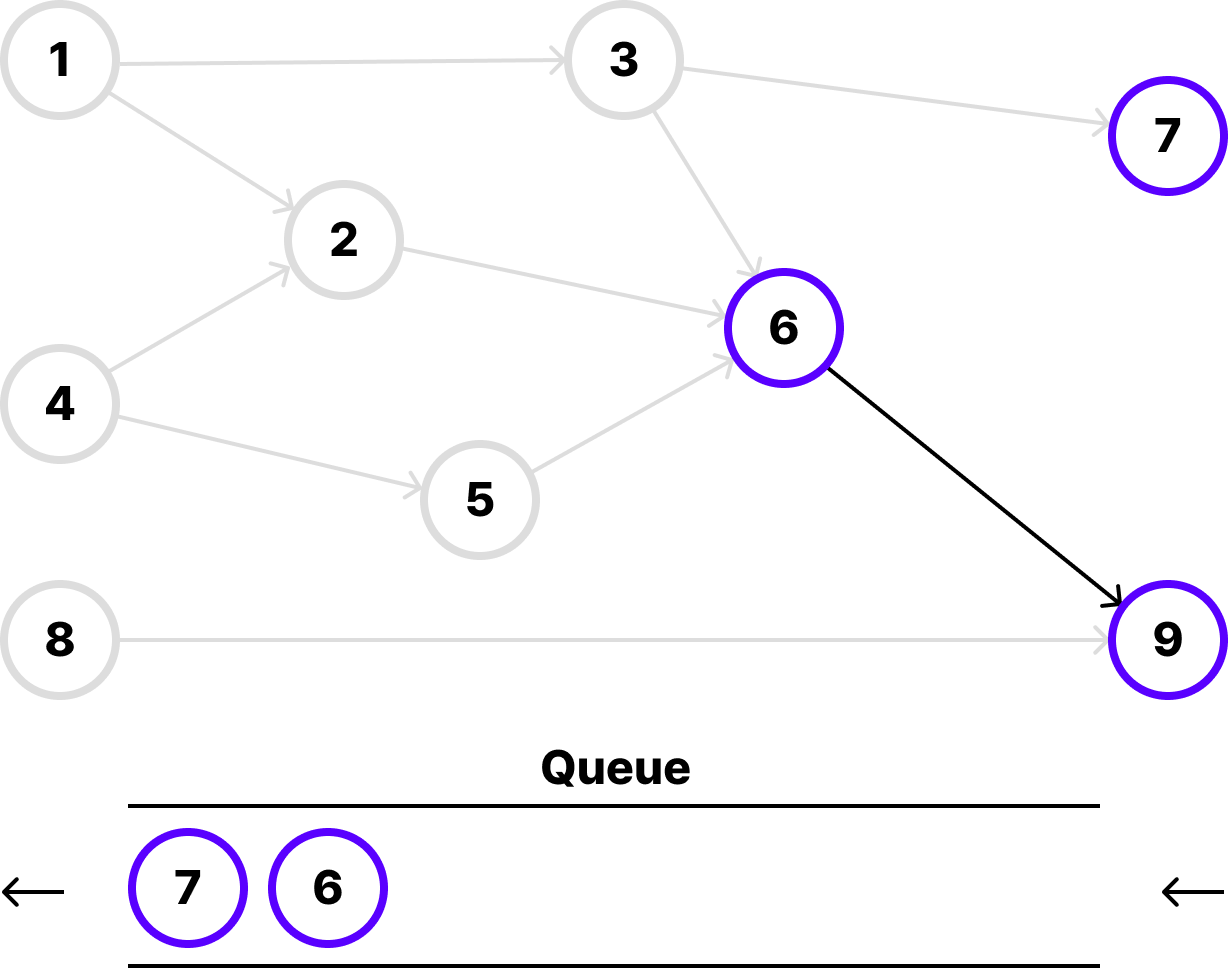
5번 노드를 추출하고 인접한 노드인 6번 노드의 진입 차수를 1 감소시킵니다. 그럼 6번 노드의 진입 차수가 0이 되어 6번 노드를 큐에 삽입할 수 있습니다.

9. 7번 노드를 추출해서 인접한 노드들 진입 차수 감소

7번 노드를 추출합니다. 인접한 노드가 없으므로 추가적인 동작은 없습니다.

10. 6번 노드를 추출해서 인접한 노드들 진입 차수 감소

6번 노드를 추출하고 인접한 9번 노드의 진입 차수를 1 감소시킵니다. 그리고 9번 노드를 큐에 추가합니다.

이제 모든 진입 차수가 0이 되었으므로 진입 차수의 변화는 없습니다.

11. 9번 노드를 추출하면서 종료

이렇게 위상 정렬이 종료되었습니다.

이렇게 노드를 추출한 순서가 곧 그래프의 위상 정렬한 결과가 됩니다.

위상 정렬 결과
(1) → (4) → (8) → (3) → (2) → (5) → (7) → (6) → (9)

Kahn's 알고리즘 실제 구현 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;
import java.util.StringTokenizer;

public class Main_Topological_Sort {
    static int n, m;
    static List<List<Integer>> list = new ArrayList<>();
    static int top[];

    static StringBuilder sb = new StringBuilder();

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		
        // 노드 수와 간선 수 입력
        StringTokenizer st = new StringTokenizer(br.readLine(), " ");
        n = Integer.parseInt(st.nextToken());
        m = Integer.parseInt(st.nextToken());

        // 진입 차수 저장 배열 초기화
        top = new int[n+1];

        // 인접 리스트 초기화
        for(int i = 0; i <= n; i++) {
            list.add(new ArrayList<>());
        }

        for(int i = 0; i < m; i++) {
            st = new StringTokenizer(br.readLine(), " ");
            int start = Integer.parseInt(st.nextToken());
            int end = Integer.parseInt(st.nextToken());

            list.get(start).add(end);
			
            // 진입 차수 갱신
            // start가 아닌 end를 증가시키는 것이 핵심
            top[end]++;
        }

        // 위상 정렬
        topologicalSort();

        // 출력
        System.out.println(sb.toString().trim());
    }

    private static void topologicalSort() {
        Queue<Integer> q = new ArrayDeque<>();

        // 진입 차수가 0인 노드 큐에 전부 추가
        for(int i = 1; i <= n; i++) {
            if(top[i] == 0) {
                q.offer(i);
            }
        }

        while(!q.isEmpty()) {
            int poll = q.poll();

            // 큐에서 추출한 노드 버퍼에 추가
            sb.append(poll+" ");

            for(int out : list.get(poll)) {
                // 추출한 노드와 인접한 노드의 진입 차수 감소
                top[out]--;
                // 만약 진입 차수가 0이라면 방문 가능하므로 큐에 추가
                if(top[out] == 0) {
                    q.offer(out);
                }
            }
        }
    }
}

입력
9 10
1 2
1 3
2 6
3 6
3 7
4 2
4 5
5 6
6 9
8 9

출력
1 4 8 3 2 5 7 6 9

구현 코드는 생각보다 간단합니다. 다른 BFS 코드처럼 인접 리스트에 그래프 정보를 저장해줍니다. 이때 top[end]++; 문을 반드시 작성해야합니다. 이 코드가 각 노드에 대한 진입 차수를 갱신하는 코드입니다.

그리고 큐 자료구조를 생성한 뒤 초기에 진입 차수가 0인 노드를 전부 큐에 추가합니다. 다음으로 위에서 봤던 알고리즘 동작 방식대로 인접한 노드들에 대해 진입 차수를 1씩 감소시키고(top[out]--), 진입 차수가 0인 노드는 큐에 추가합니다.

큐에서 노드를 추출할 때마다 버퍼에 append하고 마지막에 출력합니다.

약간의 팁으로 아래의 for문에서 후위 증감연산자를 전위 증감연산자로 변경해서 한 줄로 작성할 수 있습니다.

for(int out : list.get(poll)) {
    if(--top[out] == 0) {
        q.offer(out);
    }
}

마치며

기본적인 위상 정렬을 연습하기 위한 연습 문제는 아래와 같습니다.

2252번 줄세우기 : https://www.acmicpc.net/problem/2252
1766번 문제집 : https://www.acmicpc.net/problem/1766

위상 정렬에 DP를 더한 문제도 유명하니 풀어보는 것을 추천드립니다!

14567번 선수 과목 : https://www.acmicpc.net/problem/14567
1516번 게임 개발 : https://www.acmicpc.net/problem/1516
1005번 ACM Craft : https://www.acmicpc.net/problem/1005

그래프 공부할 때 위상 정렬 알고리즘 분류를 많이 봤었는데 이름부터 너무 겁나서 알아볼 생각도 안 했었습니다. 그런데 다른 그래프 알고리즘을 전부 이해해서 그런지 모르겠지만 위상 정렬 알고리즘은 너무나도 간단했습니다! 저처럼 처음 위상 정렬을 접한 분들도 차근차근 읽다보면 금방 이해할 것이라 믿습니다ㅎㅎ 다들 화이팅입니다! 😊

이상 궁금한 점이나 피드백은 댓글로 부탁드립니다!

'Algorithm > Graph' 카테고리의 다른 글

[Algorithm] 최소 신장 트리를 구하는 Prim 알고리즘 with JAVA (1)	2025.06.16
[Algorithm] Bellman-Ford 알고리즘 with JAVA (0)	2025.05.19
[Algorithm] 0-1 BFS 알고리즘 with JAVA (1)	2025.05.15
[Algorithm] Dijkstra 알고리즘 with JAVA (0)	2025.05.12
[Algorithm] BFS 알고리즘 with JAVA (0)	2025.05.09

현재글[Algorithm] 위상 정렬(Topological Sort)을 위한 Kahn's Algorithm with JAVA

jundyu 님의 블로그

현재는 알고리즘과 Java 언어 위주로 블로그를 작성하고 있습니다. 백엔드 개발자를 준비 중입니다.

Today :
Yesterday :

jundyu 님의 블로그

[Algorithm] 위상 정렬(Topological Sort)을 위한 Kahn's Algorithm with JAVA

들어가며