
들어가며
그래프는 제가 가장 좋아하는 알고리즘 분류입니다! 그래프 이론을 배우고 나면 단순한 자료 구조를 넘어서, 너비 우선 탐색, 깊이 우선 탐색, 최단 경로 탐색, 교착상태 판별 등 다양한 알고리즘 문제를 해결할 수 있게 됩니다.
이번 포스트에선 그래프가 무엇인지, 그래프는 어떤 방식으로 표현되는지, 그래프는 어떤 유형이 있는지, 마지막으로 그래프를 탐색하는 알고리즘에 대해 다뤄보려고 합니다. 이론 위주로 다루기 때문에 특정 언어에 국한되지 않습니다.
그래프 이론: Graph Theory
1. 그래프란

그래프는 정점과 간선으로 이루어진 자료구조입니다. 쉽게 말하면 점과 다른 두 점을 서로 연결하는 선으로 이루어진 도형입니다.
2. 그래프의 특징
그래프는 비선형적 구조입니다. 따라서 현실 세계의 다양한 관계를 모델링할 수 있습니다. 여기서 비선형적 구조란 데이터가 여러 방향으로 뻗어 있는 구조를 말합니다. 반대로 선형적 구조는 배열이나 스택, 큐와 같이 데이터가 일렬로 나열된 구조를 말합니다.
또한, 그래프에는 양방향 또는 단방향 그래프가 존재합니다. 양방향 그래프에서 간선이 존재하는 두 노드는 서로 연결되어 있지만 무방향 그래프에선 주어진 방향으로만 연결되어 있습니다.
마지막으로, 그래프의 간선에 가중치가 존재할 수 있습니다. 가중치가 존재하는 경우 가중치 그래프, 존재하지 않는 경우 비가중치 그래프라고 부릅니다. 참고로 가중치가 존재하냐에 따라 특정 노드에서 목적지 노드까지의 최소 비용을 구하는 알고리즘이 달라집니다.
3. 그래프의 표현 방식
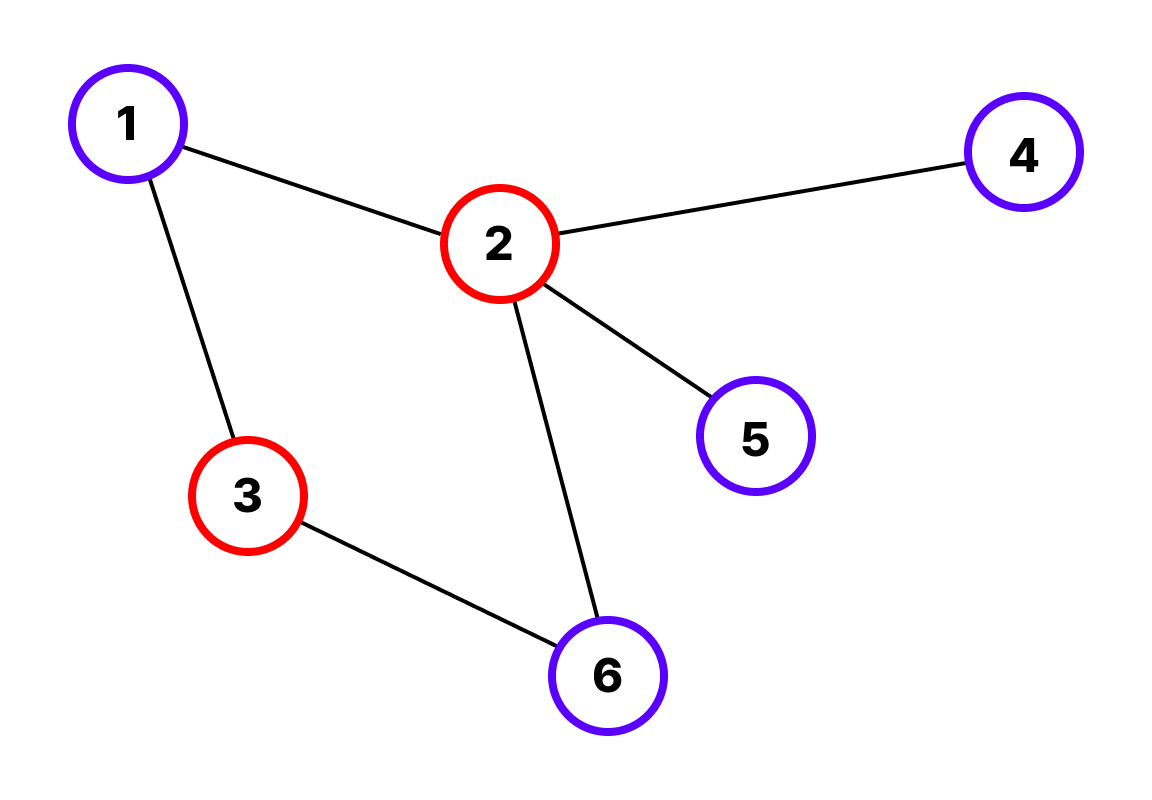
그래프는 크게 리스트 형태나 행렬 형태로 표현할 수 있습니다. 아래의 양방향 비가중치 그래프를 바탕으로 각각의 표현 방식을 알아보겠습니다.

1. 발생 행렬(Incidence Matrix)
발생 행렬은 많이 사용하지 않기 때문에 말로만 간단히 설명하고 넘어가겠습니다.
그래프의 꼭지점을 행, 간선을 열로 두고 간선과 꼭지점과의 발생 관계를 나타낸 행렬입니다. 꼭지점의 개수가 n이고 간선의 개수가 m이라면 n*m 크기의 발생 행렬이 만들어집니다.
2. 인접 리스트(Adjacency List)
각 정점에 연결된 정점들을 이중 리스트로 저장하는 방식입니다. 존재하는 간선에 대해서만 저장하기 때문에 메모리를 효율적으로 사용할 수 있습니다.
자바의 경우 List<List<Integer>> graph의 형태로 선언합니다.
List<Integer>[] graph로 표현하면 안 될까?
자바는 제네릭 타입의 배열을 직접 생성하는 것을 허용하지 않습니다. 성능에도 큰 차이가 없기 때문에 타입 안정성을 위해 이중 리스트를 사용하는 것을 권장합니다.
아래의 그림처럼 특정 노드에서 다른 노드로 간선이 존재하는 경우 각각의 노드마다 연결된 노드를 리스트에 추가합니다.
| 기준 노드 | 연결된 노드 |
| 1 | 2 3 6 |
| 2 | 1 4 5 6 |
| 3 | 1 4 |
| 4 | 2 3 8 |
| 5 | 2 7 |
| 6 | 1 2 7 |
| 7 | 5 6 8 9 |
| 8 | 4 7 9 |
| 9 | 6 7 8 |
1번 노드는 2, 3, 6번 노드와 간선으로 연결되어 있기 때문에 1 | 2 3 6으로 저장되었습니다. 나머지 8개의 노드 전부 마찬가지입니다.
3. 인접 행렬(Adjacency Matrix)
인접 행렬은 정점 간의 연결 여부를 2차원 배열로 표현하는 방식입니다. 특정 노드와 다른 노드 간의 연결 여부를 빠르게 확인할 수 있지만 모든 노드 관계에 대한 정보를 저장하므로 메모리 사용량이 많습니다.
자바의 경우 비가중치 행렬은 boolean[][] graph, 가중치 행렬은 int[][] graph와 같이 선언합니다. int 타입으로 선언한 인접 행렬은 가중치 값으로 저장되고, 간선이 존재하지 않는 경우엔 ∞값으로 저장합니다.
아래의 표는 예시 그래프를 인접 리스트 대신 인접 행렬로 표현한 것입니다.
| 구분 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 5 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 6 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 8 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
일반적으로 인접 행렬에서 자기 자신과의 연결 여부(=주대각선)는 0으로 표현합니다.
4. 그래프의 종류
다음 그래프들은 그래프의 특수한 유형에 대한 분류입니다.
1. 완전 그래프(Complete Graph)
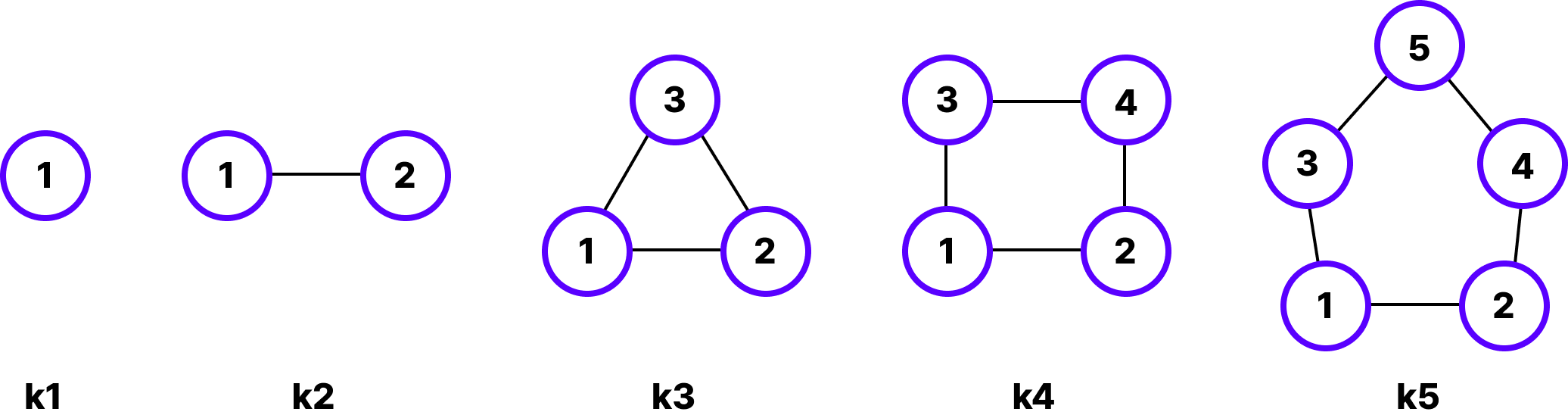
그래프에 속한 모든 정점이 다른 정점과 인접한 그래프.
즉, n개의 정점을 가진 완전 그래프는 nC2개의 간선을 가지고, Kn으로 표현합니다.
2. 이분 그래프(Bipartite Graph)
정점을 두 집합으로 나누었을 때, 각 간선이 항상 서로 다른 집합을 연결하는 그래프.
쉽게 말하면 임의의 정점 하나를 정해서 색칠하고, 인접한 정점을 다른 색으로 번갈아가면서 칠할 때 오차없이 하나의 색으로 칠해진다면 이분 그래프라고 합니다.
이분 그래프는 홀수 길이의 사이클을 가질 수 없는 것이 특징입니다. 일반적으로 좌우 팀 구성하는 문제에 많이 사용합니다.
3. 완전 이분 그래프(Complete Bipartite Graph)

이분 그래프임과 동시에 두 집합의 가능한 모든 간선의 조합이 존재하는 경우 완전 이분 그래프라고 합니다. 집합 a의 개수가 2이고 집합 b의 개수가 3이면 간선의 개수는 2*3으로 6개가 됩니다.
4. 정규 그래프(Regular Graph)

모든 정점의 차수가 동일한 그래프입니다.
간선의 개수가 모두 n개인 경우 n-정규 그래프라고 부릅니다. 무방향 그래프에선 연결된 간선의 수가 동일하면 되고, 방향 그래프에선 일반적으로 진입 차수와 진출 차수가 동일하면 정규 그래프입니다.
위의 예시는 꼭지점이 5개일 때 가능한 모든 정규 그래프를 나타냈습니다.
완전 그래프와 정규 그래프는 뭐가 다른 걸까?
완전 그래프는 모든 정점끼리 간선으로 연결되어야하고, 정규 그래프는 간선이 모두 연결될 필요는 없지만 각 정점마다 연결된 간선의 개수가 일치해야합니다.
즉, 완전 그래프는 정규 그래프이지만 정규 그래프는 완전 그래프가 아닐 수 있습니다.
5. 트리
트리에 관한 내용이 많아서 따로 분류했습니다. 아래의 글을 참고 부탁드립니다.
추가 예정!
5. 그래프 용어 정리
마지막으로 앞서 나온, 그리고 그래프 이론에서 자주 사용되는 용어들을 정리하겠습니다.
1. 그래프 구성
- 정점(Vertex) : 데이터를 담는 기본 단위. 꼭지점
- 간선(Edge) : 정점 간의 연결
- 차수(Degree) : 정점에 연결된 간선의 수
- 진입 차수(In-degree) : 방향 그래프에서 정점으로 들어오는 간선의 수
- 진출 차수(Out-degree) : 방향 그래프에서 정점에서 나가는 간선의 수
- 가중치(Weight) : 간선에 부여된 비용, 거리, 시간 등의 값
- 사이클(Cycle) : 시작 정점으로 다시 돌아오는 닫힌 경로
- 루프(Loop) : 정점이 자기 자신과 연결되어 있는 간선
2. 그래프 종류
- 방향/무방향 그래프 : 간선에 방향이 존재하는/존재하지 않는 그래프
- 가중치/비가중치 그래프 : 간선에 값이 존재하는/존재하지 않는 그래프
- 연결/비연결 그래프 : 모든/일부 정점이 서로 연결되어 있는 그래프
- 밀집 그래프 : 노드 수에 비해 간선의 수가 매우 많은 그래프
- 희소 그래프 : 간선의 수가 매우 적은 그래프
- 트리 : 사이클이 없고 연결된 무방향 그래프
- 완전 그래프 : 모든 정점이 서로 연결된 그래프
- 이분 그래프 : 정점을 두 그룹으로 나누고, 간선은 그룹 간에만 존재하는 그래프
- 완전 이분 그래프 : 이분 그래프이면서 두 그룹의 모든 정점이 서로 연결된 그래프
- 정규 그래프 : 모든 정점의 차수가 동일한 그래프
- 부분 그래프 : 원래 그래프의 일부 정점과 간선으로 구성된 그래프
- 평면 그래프 : 그래프의 모든 변이 교차하지 않게 그릴 수 있는 그래프
3. 그래프 표현
- 발생 행렬 : 꼭지점과 간선의 발생 관계로 표현하는 행렬
- 인접 리스트 : 각 정점에 연결된 간선을 이중 리스트의 형태로 저장
- 인접 행렬 : 정점의 모든 관계에 대해 연결 여부를 표시한 2차원 배열
그래프 탐색: Graph Search
앞서 그래프에 대한 정의와 그래프를 표현하는 방식과 그래프의 정보를 저장하는 방식들을 배웠습니다. 이젠 그래프가 주어졌을 때 그래프의 정보를 파악하는 방법을 알아보겠습니다.
그래프를 탐색하는 목적은 다양하고 목적에 따라 각기 다른 탐색 알고리즘이 존재합니다. 각 알고리즘을 자세히 설명하면 글이 너무 길어질 것 같아서 탐색 알고리즘 별로 따로 포스팅한 뒤에 링크를 걸어두겠습니다. 시간날 때마다 작성해서 완성시켜보도록 하겠습니다.
1. BFS: Breadth First Search
이름 : 너비 우선 탐색
목적 : 무가중치 그래프에서 정점 간의 최단 거리 탐색
특징 : 큐를 사용, 방문한 노드를 다시 방문하지 않도록 방문 배열 사용
사용 예시 : 탈출구 찾기(격자형 그래프), 최단 경로(비가중치), 트리의 레벨 탐색, 최소 이동 횟수 문제
사용 불가 : 각기 다른 가중치가 존재하는 경우
[Algorithm] BFS 알고리즘 with JAVA
들어가며BFS 알고리즘을 공부하기에 앞서 그래프 이론을 먼저 공부하면 이 글을 이해하는 데 더 도움이 될 것 같습니다! 아래의 링크에 그래프 이론에 관한 개념이 잘 정리되어 있습니다. [Algorith
jundyu.tistory.com
2. DFS: Depth First Search
이름 : 깊이 우선 탐색
목적 : 경로 및 사이클 탐색, 백트래킹 기반 문제 해결
특징 : 스택 또는 재귀 호출을 사용, 한 방향으로 끝까지 탐색한 뒤 되돌아와 다른 경로 탐색
사용 예시 : 퍼즐 탐색, 미로 탐색, 그래프의 연결 요소 개수 구하기
주의 : 재귀 깊이가 너무 큰 그래프 → 재귀 스택 오버플로우
추가 예정!
3. Dijkstra
이름 : 데이크스트라(다잌스트라)
목적 : 양의 가중치 그래프에서 하나의 정점에서 다른 모든 정점까지의 최단 경로
특징 : 우선순위 큐를 사용, 가중치가 가장 낮은 정점부터 탐색, 그리디 기반 알고리즘
사용 예시 : 지도에서 목적지까지 가장 빠른 경로
사용 불가 : 음수 가중치 또는 음수 사이클이 존재하는 그래프
[Algorithm] Dijkstra 알고리즘 with JAVA
들어가며벌써 3번째 그래프 탐색 알고리즘에 관한 글을 쓰게 되었습니다. 이번 글 역시 아래의 링크를 통해 그래프 이론을 먼저 숙지하고 읽는 겻을 추천드립니다. [Algorithm] 그래프 이론 및 그래
jundyu.tistory.com
4. 0-1 BFS
이름 : 0-1 너비 우선 탐색
목적 : 가중치가 0또는 1인 그래프에서 시작 노드의 최단 거리 탐색
특징 : 덱을 사용, 방문한 노드를 다시 방문하지 않도록 방문 배열 사용, 시간 복잡도 O(V + E)
사용 예시 : 가중치가 1이거나 존재하지 않는 그래프에서 사용
사용 불가 : 가중치가 0 또는 1이 아닌 값이 존재하는 모든 그래프
[Algorithm] 0-1 BFS 알고리즘 with JAVA
들어가며이번 글은 그래프 탐색에 관한 글로 읽기 전에 아래의 링크에서 그래프 이론을 숙지하고, 너비 우선 탐색 및 데이크스트라 알고리즘을 먼저 익히고 나면 정말 쉽게 배울 수 있습니다. [A
jundyu.tistory.com
5. Bellman-Ford
이름 : 벨만 포드
목적 : 음의 가중치 그래프에서 하나의 정점에서 다른 정점까지의 최단 거리 탐색, 음수 사이클 여부 판별
특징 : 모든 간선을 반복적으로 확인하며 거리 갱신, 시간복잡도 O(V x E)
사용 예시 : 환율 차익 탐지, 음수 사이클 판별, 비용이 마이너스인 경로 계산
사용 불가 : 간선이 많고, 가중치가 모두 양수인 그래프 → 다잌스트라 알고리즘이 훨씬 빠름
[Algorithm] Bellman-Ford 알고리즘 with JAVA
들어가며이번 글은 벨만 포드 알고리즘에 관한 포스팅입니다. 만약 그래프 이론이나 다른 그래프 탐색 알고리즘들을 모른다면 먼저 읽어보고 오는 것을 추천합니다. 아래의 링크에 그래프 이론
jundyu.tistory.com
6. Floyd-Warshall
이름 : 플로이드 워셜
목적 : 모든 정점 쌍에 대한 최단 거리
특징 : 3중 for문으로 구현, 다이나믹 프로그래밍 기반, 시간복잡도 O(V^3)
사용 예시 : 도시 간 최소 거리 계산, 경로 테이블 생성
사용 불가 : 무방향 그래프에서 음의 가중치가 존재하는 그래프, 방향 그래프에서 음의 사이클이 존재하는 그래프, 정점 수가 너무 많은 그래프
[Algorithm] Floyd-Warshall 알고리즘 with JAVA
들어가며플로이드 워셜(Floyd-Warshall) 알고리즘은 모든 정점 쌍 사이의 최단 거리를 구하는 알고리즘입니다. 3중 for문을 사용해서 전체 경로에 대해 지나칠 수 있는 노드를 점차 확장하며 가장 적
jundyu.tistory.com
7. Topological Sort - Kahn's Algorithm
이름 : 위상 정렬(Kahn's Algorithm)
목적 : 순서가 정해진 작업을 선형적으로 정렬
특징 : 큐 또는 DFS로 구현 가능, 진입 차수가 0인 노드부터 순서대로 제거하며 정렬
사용 예시 : 우선순위가 존재하는 작업 스케줄링
주의 : 방향 비순환 그래프에서만 사용 가능
[Algorithm] Kahn's Algorithm for Topological Sort with Java
들어가며제목에서 알 수 있듯이 이번 글은 위상 정렬을 위한 Kahn's 알고리즘에 대한 글입니다. 그래프와 관련된 알고리즘이므로 아래의 그래프 이론과 해당 글에 연계된 그래프 탐색 알고리즘
jundyu.tistory.com
8. Kruskal
이름 : 크루스칼
목적 : 최소 신장 트리(MST)를 구함 → 간선 정렬 기반
특징 : 간선을 가중치 순으로 정렬한 후, 사이클을 만들지 않도록 최소 간선 선택하는 방식
사용 예시 : 희소 그래프이면서 간선 가중치의 정렬이 용이한 경우, MST를 여러 번 구해야하는 경우
주의 : 간선이 매우 많고 밀집 → 정렬 비용 큼
추가 예정!
9. Prim
이름 : 프림
목적 : 최소 신장 트리(MST)를 구함 → 정점 확장 기반
특징 : 우선순위 큐를 사용, 정점 기준으로 연결된 가장 작은 간선부터 확장
사용 예시 : 네트워크/통신망 구축, 간선이 많고 밀집된 그래프
[Algorithm] 최소 신장 트리를 구하는 Prim 알고리즘 with JAVA
들어가며이번 글은 최소 신장 트리를 구하는 알고리즘 중 하나인 Prim에 대해 설명하는 글입니다. 글을 읽기 전에 아래의 링크에서 그래프 이론 및 그래프 탐색 글을 읽어보는 것을 추천합니다. [
jundyu.tistory.com
.
.
.
마치며
전부터 그래프 알고리즘에 빠져서 하나씩 파고드는 중인데 갈수록 재밌습니다. 그런데 글과 그림으로만 설명하기 쉽지 않네요.. 글 하나 쓸 때마다 체력 소모가 엄청나요🤮 알고리즘 개념 배우고 익숙해질때까지 문제도 주구장창 풀고 있습니다. 시간이 꽤 걸리겠지만 남은 그래프 탐색 알고리즘 전부 성실하게 작성해보겠습니다!
궁금한 점이나 피드백은 댓글로 부탁드립니다!
'Algorithm > Graph' 카테고리의 다른 글
| [Algorithm] Bellman-Ford 알고리즘 with JAVA (0) | 2025.05.19 |
|---|---|
| [Algorithm] 0-1 BFS 알고리즘 with JAVA (1) | 2025.05.15 |
| [Algorithm] Dijkstra 알고리즘 with JAVA (0) | 2025.05.12 |
| [Algorithm] BFS 알고리즘 with JAVA (0) | 2025.05.09 |
| [Algorithm] Floyd-Warshall 알고리즘 with JAVA (0) | 2025.04.26 |