[Algorithm] Bellman-Ford 알고리즘 with JAVA

Algorithm/Graph

[Algorithm] Bellman-Ford 알고리즘 with JAVA

jundyu 2025. 5. 19. 20:27

들어가며

이번 글은 벨만 포드 알고리즘에 관한 포스팅입니다. 만약 그래프 이론이나 다른 그래프 탐색 알고리즘들을 모른다면 먼저 읽어보고 오는 것을 추천합니다.

아래의 링크에 그래프 이론 및 탐색에 관한 내용이 잘 나와있습니다.

[Algorithm] 그래프 이론 및 그래프 탐색

들어가며그래프는 제가 가장 좋아하는 알고리즘 분류입니다! 그래프 이론을 배우고 나면 단순한 자료 구조를 넘어서, 너비 우선 탐색, 깊이 우선 탐색, 최단 경로 탐색, 교착상태 판별 등 다양한

jundyu.tistory.com

Bellman-Ford : 벨만 포드

1. 알고리즘 명칭

Bellman-Ford라는 알고리즘의 명칭은 "Richard Bellman"와 "Lester Ford Jr."이라는 수학자의 이름에서 유래되었습니다. 벨만 포드 알고리즘이라고 불립니다.

2. 목적

벨만 포드 알고리즘의 사용 목적을 데이크스트라 알고리즘과 비교해서 설명하겠습니다.

데이크스트라 알고리즘은 음의 가중치가 없는 가중치 그래프에서 최소 비용을 구하는 알고리즘입니다. 그에 반해 벨만 포드 알고리즘은 그래프에 음의 가중치가 존재해도 최소 비용을 구할 수 있습니다. 단, 음의 사이클은 존재하면 안 됩니다. 음의 사이클이 존재하면 최소 비용이 무한히 작아지기 때문에 알고리즘을 적용할 수가 없어집니다.

결론적으로 벨만 포드 알고리즘은 음의 가중치가 존재할 때 하나의 노드에서 출발해 각 노드까지의 최소 비용을 구할 수 있고, 음의 사이클을 탐지할 수 있는 알고리즘입니다.

3. 특징

1. 음수 가중치 가능 & 음수 사이클이 존재하면 불가능

위에서 이미 언급했지만 음의 가중치가 가능한 대신 음수 사이클이 존재하면 최소 비용은 무한히 작아질 수 있습니다. 따라서 벨만 포드 알고리즘에선 최소 비용을 구한 뒤에 음수 사이클이 존재하는 지 탐지하는 과정까지 필요합니다.

3. 시간 복잡도는 O(V * E)

벨만 포드의 시간 복잡도는 데이크스트라의 시간 복잡도보다 훨씬 큰 것을 알 수 있습니다. 따라서 가중치에 음수가 존재하지 않는다면 데이크스트라 알고리즘을 사용하는 것이 훨씬 유리합니다.

4. 그래프 탐색이 아닌 DP 알고리즘의 일종

벨만 포드는 엄밀히 따지면 그래프 탐색이 아닙니다. 아래에서 알고리즘 동작 과정을 보면 알겠지만 매번 모든 간선 리스트를 확인하면서 최소 비용을 갱신하는 DP 방식입니다.

Bellman-Ford 알고리즘 설명 전

벨만 포드 알고리즘의 구체적인 동작을 보기 전에 알고가야할 것들이 있습니다.

1. 간선 리스트(Edge List)

간선 리스트에 대해 간단하게 짚고 넘어가겠습니다.

간선 리스트란?

그래프에 존재하는 모든 간선을 리스트 형태로 저장하는 방식입니다. 인접 리스트가 하나의 정점에서 다른 정점으로 이동 가능한 모든 간선 정보를 저장한 것과 약간 다르게 간선 리스트는 출발 노드, 도착 노드, 가중치 형태로 리스트에 저장합니다.
간선 리스트는 메모리의 효율이 좋은 반면 특정 간선을 찾는 시간 복잡도는 비효율적입니다.

자세한 설명은 서론의 링크에 있는 그래프 이론 포스팅을 참고바랍니다.

2. 정점 간의 최대 거리는 n-1

정점의 개수가 n개일 때 1번 노드에서 n번 노드로 이동하기 위한 최대 간선 수는 몇개일까요? n-1개입니다. 아래의 그림을 참고하면 훨씬 와닿을 것 같습니다.

위의 그림처럼 노드의 개수가 9일 때 1번 노드와 9번 노드를 아무리 떨어트려놔도 최대 거리는 8인 것을 알 수 있습니다. 즉, 노드의 개수가 n일 때 노드의 최대 거리는 n-1입니다.

3. n-1개의 각 간선을 기준으로 점층적 확장

위의 1, 2번 개념을 통해 벨만 포드의 핵심 개념을 알 수 있습니다. 벨만 포드 알고리즘은 각 n-1개의 간선을 기준으로 가능한 모든 간선을 하나씩 확장하면서 최소 비용을 갱신합니다. 간선 자기 자신을 기준으로 아무리 멀어야 n-1만큼 떨어져있기 때문에 n-1번만큼만 반복하면서 비용을 갱신하면 됩니다.

추가로 비용의 갱신이 한 번도 없었다면 n-1번까지 반복하지 않고 그 즉시 반복문을 종료해도 됩니다. 이미 간선 자기 자신과 가장 멀리 떨어진 간선까지 다 확인했다는 의미이기 때문입니다.

4. 비용 갱신 점화식

점화식은 아래와 같습니다.

if(dist[edge.start] != INF && dist[edge.start] + out.w < dist[edge.end]) {
    dist[edge.end] = dist[edge.start] + out.w;
}

조건문 2번째 : 만약 간선의 출발점까지의 비용 + 가중치가 간선의 끝점까지의 비용보다 작다면 전자의 비용으로 갱신합니다.
조건문 1번째 : 간선의 출발점의 비용이 무한대이면 갱신할 필요가 아예 없습니다.

후술할 실제 구현 코드에서 자세하게 설명하겠습니다. 지금은 점화식을 간략하게만 숙지하고 있으면 됩니다.

그림으로 보는 벨만 포드 과정

위의 그래프는 제가 임의로 1번부터 9번까지의 노드에 음수가 포함된 방향 그래프를 그린 예시입니다. 원활한 설명을 위해 우선 음의 사이클이 없는 그래프로 만들었습니다.

1번 노드에서 시작하여 모든 노드로 이동하는 최소 비용을 구해보겠습니다. 다른 최소비용을 구하는 알고리즘과 마찬가지로 cost(또는 dist) 배열이 필요합니다.

그리고 벨만 포드 알고리즘에선 간선 리스트가 어떤 순서로 주어지냐에 따라 빠르게 끝날 수도 있고 n-1번에 가깝게 순회를 해서 최소 비용을 알아내야할 수도 있습니다.

이번엔 아래처럼 순차적으로 간선의 정보가 주어졌다고 가정하겠습니다.

간선 리스트

9 15 // node, edge
1 2 3
1 3 3
1 5 4
2 5 -1
3 2 5
3 4 3
3 8 1
4 6 6
4 7 -1
5 6 4
6 3 -2
6 9 -5
7 9 4
8 9 7
9 4 4

1. 먼저 비용 배열을 무한대로 초기화 후 시작

각 노드에 대한 최소 비용을 구하는 알고리즘이기 때문에 마찬가지로 비용 배열을 무한대로 초기화하면서 시작합니다. 빨간 글씨가 각 노드로 이동하는 최소 비용을 의미하고 현재 무한대 값으로 초기화되어 있습니다.

그리고 시작 노드의 비용은 0으로 초기화합니다.

2. 1차 간선 리스트 순회

i) start = 1, end = 2, weight = 3

1차 간선 리스트 순회에서 간선 리스트의 첫번째 간선 정보를 확인합니다.

시작 노드가 1인데 최소 비용이 0이므로 true이고, dist[edge.start] + weight = 3이 dist[edge.end] = ∞보다 작기 때문에 갱신이 일어납니다.

ii) start = 1, end = 3, weight = 3

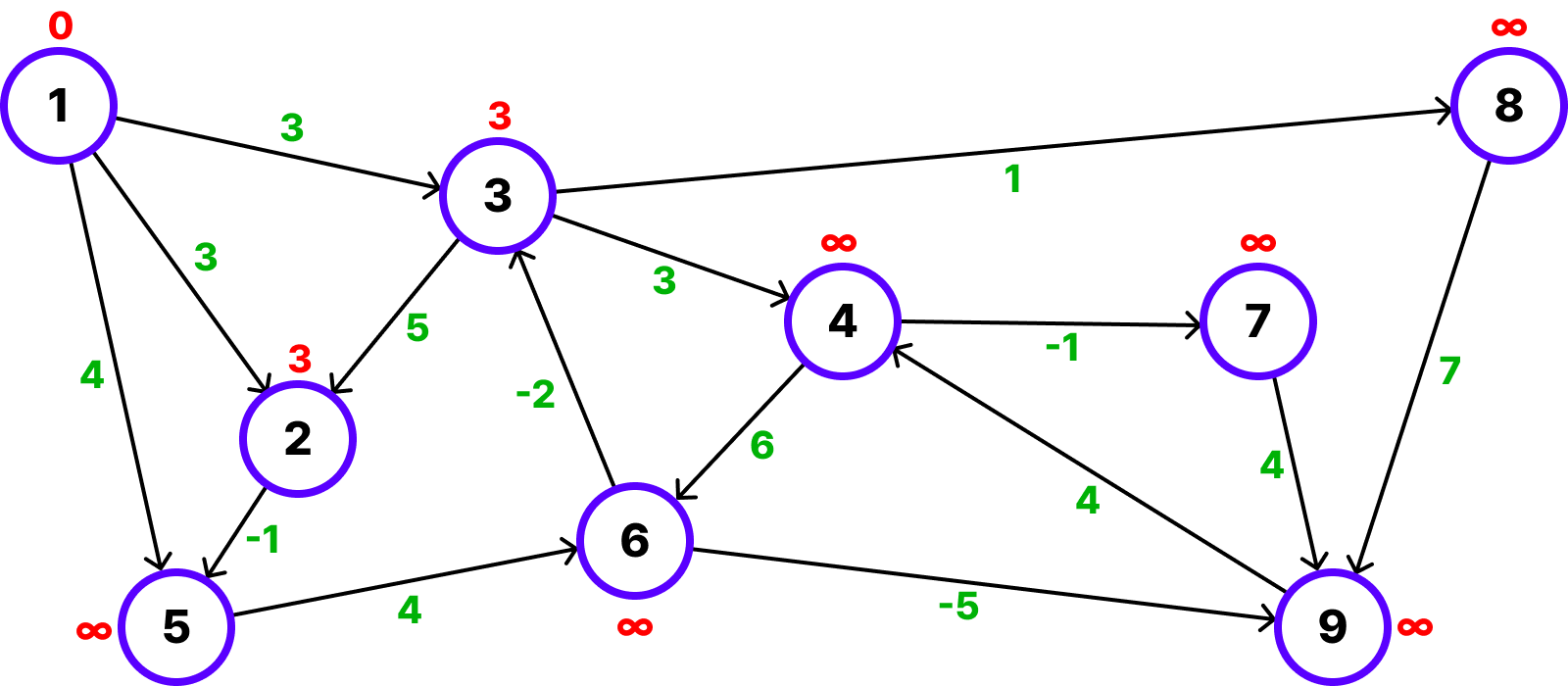
i의 경우와 마찬가지로 시작 노드의 최소 비용이 ∞이 아니고, dist[edge.start] + weight = 3이 dist[edge.end] = ∞보다 작기 때문에 갱신이 일어납니다.

이상 수식을 따로 적지 않고 값만 적겠습니다. 그리고 최소 비용이 ∞였던 노드를 방문하는 경우는 간단히 설명하고 넘어가겠습니다.

iii) start = 1, end = 5, weight = 4

i, ii의 경우와 마찬가지로 시작 노드의 최소 비용이 ∞이 아니고, 4가 ∞보다 작기 때문에 갱신이 일어납니다.

iv) start = 2, end = 5, weight = -1

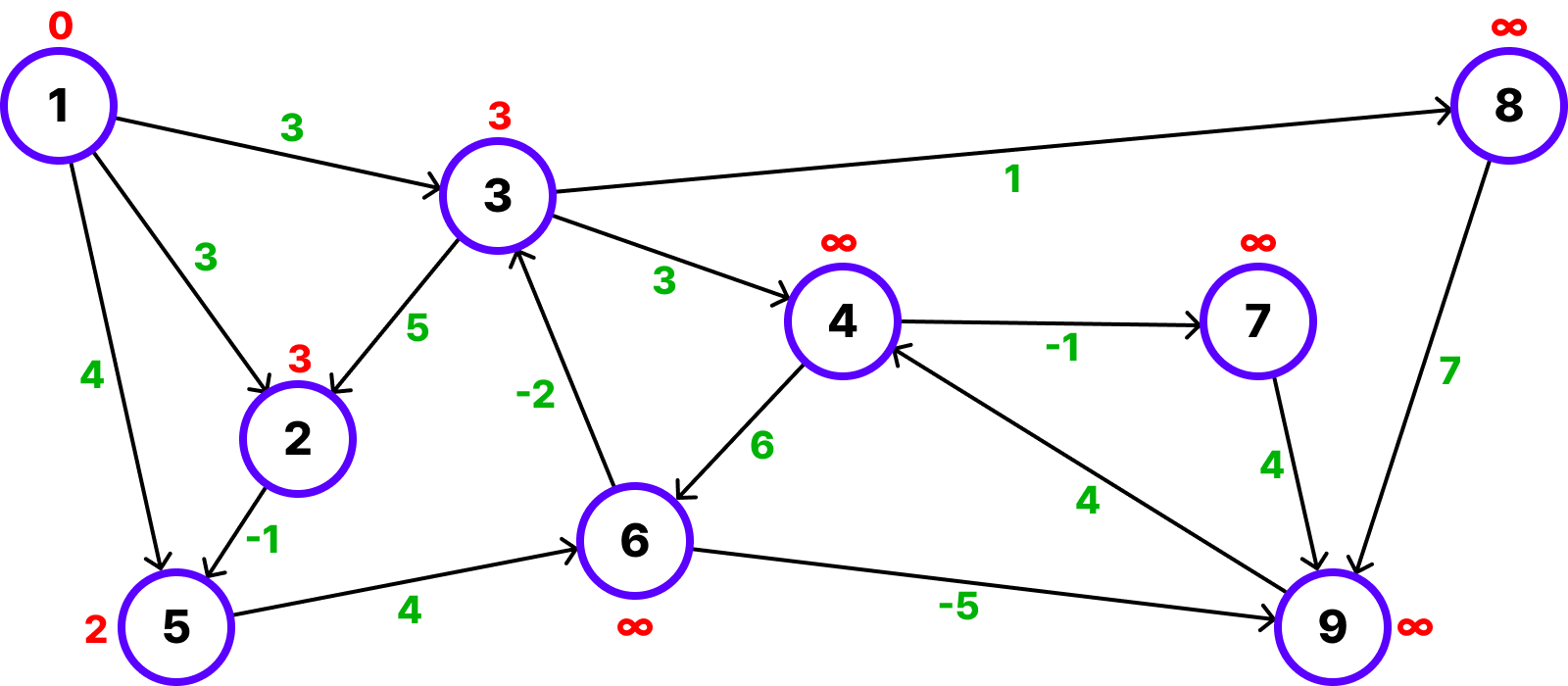
마찬가지로 시작 노드의 최소 비용이 ∞이 아니고, 2가 4보다 작기 때문에 갱신이 일어납니다.

v) start = 3, end = 2, weight = 5

해당 간선에선 갱신이 일어나지 않습니다. 3번 노드까지의 비용은 3이고 간선의 가중치는 5라서 2번 노드까지의 비용 3보다 커서 이동할 필요가 없습니다.

vi) start = 3, end = 4, weight = 3

4번 노드의 최소 비용이 현재 ∞이므로 갱신 가능합니다.

vii) start = 3, end = 8, weight = 1

3번 노드에서 8번 노드를 잇는 간선도 마찬가지로 4로 갱신가능합니다.

viii) start = 4, end = 6, weight = 6

4번 노드에서 6번 노드로 가는 것도 마찬가지로 ∞를 12로 갱신가능합니다.

ix) start = 4, end = 7, weight = -1

마찬가지로 4번 노드에서 7번 노드로 가는 것도 비용 5로 갱신 가능합니다.

x) start = 5, end = 6, weight = 4

5번 노드로의 최소 비용은 2입니다. 그리고 5번 노드에서 6번 노드로 이어진 간선의 가중치는 2입니다. 6번 노드로의 최소 비용 12보다 작기 때문에 dist[6] = 6으로 갱신됩니다.

xi) start = 6, end = 3, weight = -2

해당 간선에선 갱신이 일어나지 않습니다. 갱신하려는 비용 4가 현재의 최소 비용 3보다 크기 때문에 갱신할 필요가 없습니다.

xii) start = 6, end = 9, weight = -5

6번 노드로의 최소 비용은 6이고 가중치는 -5이므로 9번 노드로의 최소 비용은 1로 갱신됩니다.

xiii) start = 7, end = 9, weight = 4

xi의 경우와 같은 이유로 해당 간선에선 갱신이 일어나지 않습니다.

xiv) start = 8, end = 9, weight = 7

xiii의 경우와 같은 이유로 해당 간선에선 갱신이 일어나지 않습니다.

xv) start = 9, end = 4, weight = 4

1회차 순회의 마지막 간선입니다. 9번 노드로의 최소 비용이 1인데 4번 노드로의 가중치가 4이므로 6보다 작습니다. 따라서 4번 노드로의 가중치가 갱신됩니다.

3. 2차 간선 리스트 순회

i) start = 4, end = 7, weight = -1

갱신이 일어나지 않는 간선들은 전부 건너뛰고, 해당 간선을 살펴보겠습니다.

4에서 7로의 가중치가 -1이기 때문에 7번 노드로의 최소 비용은 최종적으로 4로 갱신됩니다.

4. 순회 종료

이후 추가적인 갱신이 일어나지 않습니다. 따라서 n-1회 반복할 필요 없이 즉시 종료 가능합니다.

결과적으로 1번 노드에서 각 노드까지의 최소 비용은 아래와 같습니다.

간선 리스트와 반복 횟수

위의 동작 과정에서 간선의 정보를 아래와 같이 최대한 오름차순으로 입력했습니다.

그리고 2회차까지만 갱신이 일어나고 그 후에 반복문이 종료되는 것을 봤습니다.

만약 간선 리스트의 순서와 반복문이 몇회차까지 반복되는지가 상관이 있을까요? 결론부터 말하면 입력 순서에 따라 최대 회차가 조금씩 달라집니다.

저는 예시 그래프에서 시작 노드를 1번으로 두고 노드의 숫자가 커질수록 1번 노드에서 거리가 멀어지도록 만들었습니다. 그래서 오름차순으로 입력한 간선 리스트의 갱신이 2회차 만에 끝날 수 있었던 것입니다.

그럼 동일한 그래프를 간선의 순서를 바꿔 실행해보겠습니다. 아래는 각각의 입력에 대해 각 회차별로 몇번씩 갱신이 일어나는지 테스트한 결과입니다.

왼쪽 사진은 간선의 순서를 역순으로 입력했고, 나머지 사진은 순서를 완전히 랜덤으로 입력한 결과입니다.

음의 사이클이 존재하는 경우

벨만 포드 알고리즘은 음의 사이클이 존재하는 지도 판별 가능하다고 했습니다. 이번엔 음의 사이클을 어떻게 탐지하는 건지와 음의 사이클이 왜 존재하면 안 되는건지 살펴보겠습니다.

1. 음의 사이클 탐지

최소 비용이 전부 갱신된 상태에서 간선 리스트에 대해서 한 번 더 순회를 하면 어떻게 될까요? 최소 비용은 n-1번 이내에 전부 갱신되었기 때문에 더이상의 갱신이 발생하면 안 됩니다.

하지만 음의 사이클이 존재하면 순회를 할 때마다 최소 비용이 갱신될 것입니다. 따라서 n-1번의 반복 후에 마지막으로 한 번 더 간선 리스트를 순회할 때 최소 비용이 갱신되는 순간 음의 사이클이 존재한다고 판단할 수 있습니다.

2. 음의 사이클이 존재하면 안 되는 이유

사실 음의 사이클이 존재하면 안 되는 이유는 잠깐만 생각해보면 당연합니다. 음의 사이클에서 무한히 루프를 돌아서 최소 비용이 음의 무한대로 한없이 작게 만들 수 있기 때문입니다.

벨만 포드 알고리즘 실제 구현 코드

1. Edge Class

static class Edge {
    int start, end, w;

    public Edge(int start, int end, int w) {
        this.start = start;
        this.end = end;
        this.w = w;
    }
}

간선의 정보를 담고 있는 Edge 클래스입니다.

2. 선언 및 입력

public static void main(String[] args) throws IOException {
    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

    StringTokenizer st = new StringTokenizer(br.readLine(), " ");
    int n = Integer.parseInt(st.nextToken());
    int m = Integer.parseInt(st.nextToken());

    List<Edge> list = new ArrayList<>();

    for(int i = 0; i < m; i++) {
        st = new StringTokenizer(br.readLine(), " ");
        list.add(new Edge(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken())));
    }

    long dist[] = new long[n+1];
    Arrays.fill(dist, INF);
    dist[1] = 0;
}

메인 메서드입니다. 처음 노드의 수와 간선의 수를 입력 받고, Edge 객체를 List의 형태로 저장할 list 자료구조를 선언합니다. 그리고 차례로 입력되는 간선의 정보를 list에 추가합니다.

각 노드별 최소 비용을 저장할 dist 배열을 선언하고 무한대 값으로 채워줍니다.

마지막으로 시작 노드의 최소 비용을 0으로 수정합니다.

3. 벨만 포드 핵심 로직

for(int i = 0; i < n-1; i++) {
    boolean changed = false;

    for(Edge out : list) {
        if(dist[out.start] != INF && dist[out.start] + out.w < dist[out.end]) {
            dist[out.end] = dist[out.start] + out.w;
            changed = true;
        }
    }

    if(!changed) break;
}

우선 boolean 타입의 changed 플래그는 무시하겠습니다.

앞서 언급했듯이 간선 리스트 순회는 총 n-1번 진행합니다. 그리고 간선 리스트를 for문으로 조회하면서 거리를 갱신합니다.

초반부의 점화식에서 이미 봤지만 조회한 간선의 출발 노드의 최소비용이 무한대라면 비용을 비교할 필요조차 없습니다. 또한, 출발 노드의 최소비용과 가중치의 합이 도착 노드에 현재 저장된 최소비용보다 작은 경우만 비용을 새로 갱신합니다.

이제 changed 플래그를 보겠습니다.

각 순회마다 한 번이라도 갱신한 적이 있는 지 확인하는 플래그입니다. 만약 한 번의 순회에서 한 번도 갱신한 적이 없다면 dist 배열은 이미 모두 갱신된 상태입니다. 따라서 즉시 break로 반복을 종료합니다.

4. 음의 사이클 존재 확인

for(Edge out : list) {
    if(dist[out.start] != INF && dist[out.start] + out.w < dist[out.end]) {
        System.out.println("음의 사이클 존재");
        return;
    }
}

만약 모든 갱신이 끝난 상태에서 또 갱신을 시도했는데 추가로 최소비용을 갱신할 수 있다면 음의 사이클이 존재한다는 의미입니다.

5. 최소비용 출력

for(int i = 1; i <= n; i++) {
    System.out.println("1번 노드에서 "+i+"번 노드까지의 최소 비용 : "+dist[i]);
}

1번 노드에서 각 노드까지의 최소 비용을 추가합니다.

6. 전체 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.StringTokenizer;

public class Main_Bellman_Ford {
    static final int INF = 100000000;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        StringTokenizer st = new StringTokenizer(br.readLine(), " ");
        int n = Integer.parseInt(st.nextToken());
        int m = Integer.parseInt(st.nextToken());

        List<Edge> list = new ArrayList<>();

        for(int i = 0; i < m; i++) {
            st = new StringTokenizer(br.readLine(), " ");
            list.add(new Edge(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken())));
        }

        long dist[] = new long[n+1];
        Arrays.fill(dist, INF);
        dist[1] = 0;

        for(int i = 0; i < n-1; i++) {
            boolean changed = false;

            for(Edge out : list) {
                if(dist[out.start] != INF && dist[out.start] + out.w < dist[out.end]) {
                    dist[out.end] = dist[out.start] + out.w;
                    changed = true;
                }
            }

            if(!changed) break;
        }

        for(Edge out : list) {
            if(dist[out.start] != INF && dist[out.start] + out.w < dist[out.end]) {
                System.out.println(-1);
                return;
            }
        }

        for(int i = 1; i <= n; i++) {
        	System.out.println("1번 노드에서 "+i+"번 노드까지의 최소 비용 : "+dist[i]);
        }
    }

    static class Edge {
        int start, end, w;

        public Edge(int start, int end, int w) {
            this.start = start;
            this.end = end;
            this.w = w;
        }
    }
    }

입력
9 15
1 2 3
1 3 3
1 5 4
2 5 -1
3 2 5
3 4 3
3 8 1
4 6 6
4 7 -1
5 6 4
6 3 -2
6 9 -5
7 9 4
8 9 7
9 4 4

출력
1번 노드에서 1번 노드까지의 최소 비용 : 0
1번 노드에서 2번 노드까지의 최소 비용 : 3
1번 노드에서 3번 노드까지의 최소 비용 : 3
1번 노드에서 4번 노드까지의 최소 비용 : 5
1번 노드에서 5번 노드까지의 최소 비용 : 2
1번 노드에서 6번 노드까지의 최소 비용 : 6
1번 노드에서 7번 노드까지의 최소 비용 : 4
1번 노드에서 8번 노드까지의 최소 비용 : 4
1번 노드에서 9번 노드까지의 최소 비용 : 1

마치며

마지막으로 백준에서 풀어보면 좋은 벨만 포드 알고리즘 연습 문제를 남겨놓겠습니다.

11657번 타임머신 : https://www.acmicpc.net/problem/11657
1865번 웜홀 : https://www.acmicpc.net/problem/1865

추가적으로 궁금한 점이나 피드백은 댓글로 부탁드립니다.

'Algorithm > Graph' 카테고리의 다른 글

[Algorithm] 최소 신장 트리를 구하는 Prim 알고리즘 with JAVA (1)	2025.06.16
[Algorithm] 위상 정렬(Topological Sort)을 위한 Kahn's Algorithm with JAVA (0)	2025.05.23
[Algorithm] 0-1 BFS 알고리즘 with JAVA (1)	2025.05.15
[Algorithm] Dijkstra 알고리즘 with JAVA (0)	2025.05.12
[Algorithm] BFS 알고리즘 with JAVA (0)	2025.05.09

현재글[Algorithm] Bellman-Ford 알고리즘 with JAVA

jundyu 님의 블로그

현재는 알고리즘과 Java 언어 위주로 블로그를 작성하고 있습니다. 백엔드 개발자를 준비 중입니다.

Today :
Yesterday :

jundyu 님의 블로그