
들어가며
BFS 알고리즘을 공부하기에 앞서 그래프 이론을 먼저 공부하면 이 글을 이해하는 데 더 도움이 될 것 같습니다! 아래의 링크에 그래프 이론에 관한 개념이 잘 정리되어 있습니다.
[Algorithm] 그래프 이론 및 그래프 탐색
들어가며그래프는 제가 가장 좋아하는 알고리즘 분류입니다! 그래프 이론을 배우고 나면 단순한 자료 구조를 넘어서, 너비 우선 탐색, 깊이 우선 탐색, 최단 경로 탐색, 교착상태 판별 등 다양한
jundyu.tistory.com
이번 글에선 그래프를 탐색하는 방식 중 너비 우선 탐색(BFS)에 대해 알아보겠습니다.
BFS : Breadth First Search
1. 그래프를 탐색하는 목적
일반적으로 그래프의 탐색은 특정 목적지까지의 최단 경로를 구하거나 그래프의 전체적인 구조를 파악하는 데에 있습니다. 그 중에 간선에 가중치가 존재하지 않은 경우(=가중치가 전부 동일한 경우) 너비 우선 탐색으로 최단 경로를 알아낼 수 있습니다.
2. BFS란

BFS는 Breadth First Search이고 한글로 풀어서 쓰면 너비 우선 탐색입니다. 즉, 그래프가 위의 슬라이드처럼 주어졌을 때 시작 노드부터 인접한 노드로 한 단계씩 깊어지면서 모든 정점들을 탐색하는 방식입니다.
중반부에서 더 자세히 다뤄보겠습니다.
3. BFS 알고리즘의 특징
1. Queue 자료구조를 사용하여 방문한 노드를 관리함
현재 노드에 인접한 노드를 전부 확인해서 큐에 삽입합니다. 큐의 자료구조는 선형적이므로 앞에서 뒤로 갈수록 노드의 깊이가 커집니다.
2. 모든 간선의 가중치가 동일하거나 없는 경우 최단 경로를 구함
너비 우선 탐색은 탐색의 깊이가 곧 비용을 의미하므로 가중치가 각기 다른 경우엔 최소 비용을 구할 수 없습니다. 만약 각 간선마다 다른 가중치가 부여된 경우 데이크스트라, 플로이드 워셜, 벨만 포드 등의 알고리즘으로 최단 경로를 구할 수 있습니다.
3. 노드 수가 많은 경우 공간 복잡도가 큼
인접한 노드를 전부 큐에 삽입하기 때문에 분기가 많으면 메모리가 많이 소모됩니다.
4. 이미 방문한 노드를 다시 방문하여 사이클이 생기지 않도록 방문 처리 필요함
너비 우선 탐색은 시작 노드로부터 한 단계씩 깊어지면서 인접한 노드로 접근합니다. 따라서 최초로 도달한 노드가 최단 거리임을 보장하므로 방문 처리를 해서 굳이 다른 노드에서 방문할 필요가 없도록 만듭니다.
4. 그래프 데이터의 형태
그래프 관련 알고리즘 문제를 접하다보면 그래프가 2가지 형태로 주어지는 것을 알 수 있습니다. 서론의 링크에서 계속 나오는 일반적인 그래프의 모습과 2차원 격자 형태의 그래프입니다.
둘이 그래프라는 점에서 특별한 차이는 없기 때문에 BFS 과정은 하나로 통합해서 설명하고, 구현 단계에서 자세히 비교해보겠습니다.
그림으로 보는 BFS 과정 : 일반적인 형태의 그래프
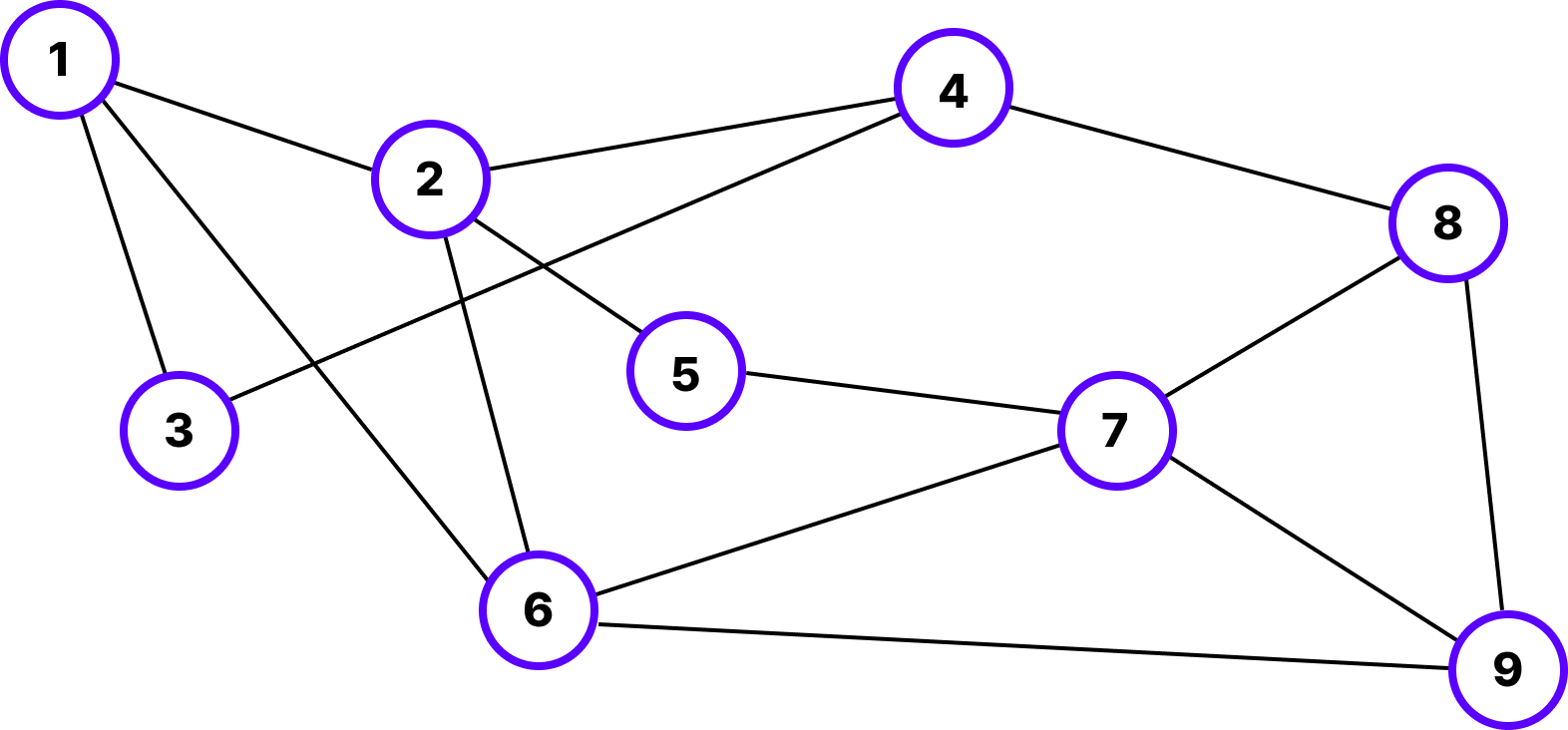
위의 그림처럼 그래프가 주어진 경우 1번 노드에서 출발해 각 노드까지의 최단 거리를 구해보겠습니다. 앞서 설명했듯이 너비 우선 탐색에는 큐와 방문 배열(boolean)이 필요합니다.
1. 큐에 1번 노드 추가 및 방문 처리

큐에 시작 노드인 1번 노드를 삽입했습니다. 그리고 1번 노드는 방문했기 때문에 보라색으로 표시해줬습니다.
1번 노드에서 1번 노드로 가기 위한 최단 거리는 0이므로 큐에 추가할 때 node=1, distance=0인 노드를 삽입했습니다.
2. 큐에서 1번 노드를 꺼내서 인접한 노드들을 큐에 삽입

큐에 1번 노드가 들어있었고, 1번 노드를 꺼내서 인접한 노드들을 전부 조회합니다. 이때 아직 방문하지 않은 노드가 존재한다면 큐에 추가합니다.
1번 노드에서 2, 3, 6번 노드로 이동할 때 간선 하나를 거쳐야하므로 거리를 +1 해주면서 큐에 추가했습니다.
3. 큐에서 2번 노드를 꺼내서 인접한 노드들을 큐에 삽입

큐의 가장 앞에 2번 노드가 들어있고, 2번 노드까지의 거리가 1이 필요했다는 것을 알 수 있습니다. 다시 큐의 가장 앞에 있는 노드인 2번 노드를 꺼내서 2번 노드와 인접한 노드들을 조회합니다. 인접한 노드는 4, 5번 노드이므로 큐에 거리를 +1 하면서 삽입합니다.
2번 노드가 6번 노드와 인접하지만 추가하지 않는 이유는 이미 방문 처리를 했기 때문입니다.
4. 큐에서 3번 노드를 꺼내서 인접한 노드들을 큐에 삽입
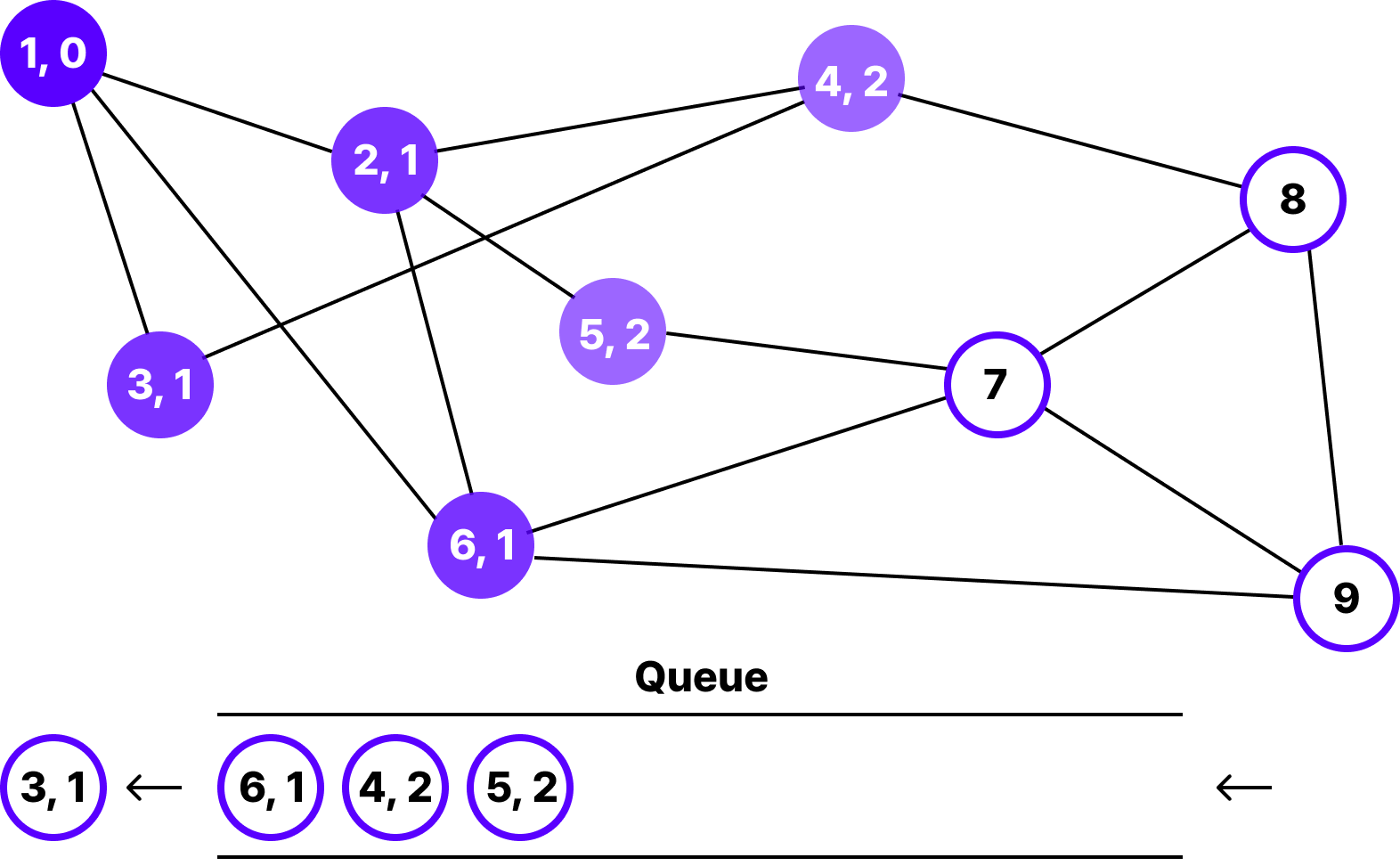
큐의 가장 앞에 3번 노드가 있지만 3번 노드와 인접한 노드 중에 방문하지 않은 노드가 없기 때문에 아무것도 추가되지 않고 넘어갑니다.
5. 큐에서 6번 노드를 꺼내서 인접한 노드들을 큐에 삽입

큐의 가장 앞에 있는 노드 6번을 꺼냈습니다. 아직 방문하지 않은 노드 중 인접한 노드는 7, 9번 노드입니다. 6번 노드까지의 거리가 1이었기 때문에 7, 9번 노드까지의 거리는 +1을 한 2입니다.
6. 큐에서 6번 노드를 꺼내서 인접한 노드들을 큐에 삽입

마지막으로 4번 노드를 꺼내서 인접한 노드를 탐색하면 8번 노드가 존재하는 것을 알 수 있습니다. 4번 노드까지의 거리가 2이므로 8번 노드까지의 거리는 +1을 한 3이 됩니다.
7. 더이상 방문 가능한 노드가 없으므로 전부 생략
9개의 노드 전부 방문했고, 최단 거리를 구했으므로 큐는 empty 상태가 되며 탐색을 종료합니다.
위의 BFS 과정을 보면 큐의 가장 앞에 있는 노드를 꺼내서 인접한 노드를 추가하는 과정이 반복적인 것을 알 수 있습니다. 그리고 큐가 비어있을 때까지 계속 반복하는 것을 알 수 있습니다. 모든 노드에 대해 최단 거리를 구했기 때문에 큐가 빌 때까지 반복했지만, 특정 노드까지의 거리를 구하고 싶은 경우에는 특정 노드에 도착하자마자 탐색을 종료하면 됩니다.
BFS 실제 구현 코드
이제 자바를 기준으로 실제로 어떻게 BFS를 구현하는지 보겠습니다. 대부분의 BFS 알고리즘 문제는 아래의 코드를 응용하는 방향으로 출제됩니다. 아래의 틀에서 문제의 출제 의도에 맞게 변형하면 됩니다.
앞서 일반적인 그래프와 2차원 격자 그래프 두 가지의 형태로 주어진다고 했기 때문에 두 경우로 나누어서 보겠습니다.
1. 일반적인 그래프
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main_BFS_General {
static int size, edge;
static List<List<Integer>> list = new ArrayList<>();
static boolean[] visit;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 그래프의 노드, 간선 수 저장
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
size = Integer.parseInt(st.nextToken());
edge = Integer.parseInt(st.nextToken());
// 방문 배열 및 인접 리스트 초기화
// 1번 노드부터 size번 노드까지 존재하기 때문에 size+1만큼 초기화
visit = new boolean[size+1];
for(int i = 0; i <= size; i++) {
list.add(new ArrayList<>());
}
for(int i = 0; i < edge; i++) {
st = new StringTokenizer(br.readLine(), " ");
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
// 양방향 그래프인 경우 인접 리스트에 아래처럼 간선 추가
list.get(start).add(end);
list.get(end).add(start);
}
// 1번 노드부터 시작해서 9번 노드까지의 최단 거리
int result= bfs(1, 9);
// 출력
System.out.println(result);
}
private static int bfs(int i, int j) {
Queue<int[]> q = new ArrayDeque<>();
// 탐색을 시작할 노드를 추가하고 현재 노드까지의 거리를 0으로 저장
q.offer(new int[] {i, 0});
// 방문 배열 갱신
visit[i] = true;
while(!q.isEmpty()) { // 큐가 빌 때까지 반복
// 큐에 들어있는 노드 추출
int[] poll = q.poll();
// 목표에 도달한 경우 거리 반환
if(poll[0] == j) {
return poll[1];
}
for(int search : list.get(poll[0])) { // 추출한 노드의 인접한 노드들 전부 방문
if(!visit[search]) { // 방문하지 않은 노드만 큐에 추가
// 방문하지 않았던 큐를 추가하되, 거리는 현재의 +1만큼 추가
q.offer(new int[] {search, poll[1]+1});
// 방문 처리
visit[search] = true;
}
}
}
// 간선이 없어 도달 불가한 경우
return -1;
}
}입력
9 14
1 2
1 3
1 6
2 4
2 5
2 6
3 4
4 8
5 7
6 7
6 9
7 8
7 9
8 9
출력
2
일반적인 그래프의 경우 List<List<Integer>> list와 같이 이중 리스트로 간선의 정보를 저장하면 됩니다.
그래프가 양방향인지 단방향인지에 따라 간선을 입력하는 방식이 달라집니다. 양방향이면 start와 end를 번갈아가면서 저장해줘야하고, 단방향인 경우 해당하는 방향만 저장하면 됩니다.
위의 예시 그림으로 입력을 했을 때 1번 노드에서 9번 노드까지의 최단 거리는 2로 정상적으로 출력되는 것을 볼 수 있습니다.
2. 2차원 격자 그래프

위의 그림처럼 2차원 격자 형태의 그래프가 주어지는 문제도 정말 많습니다. BFS 알고리즘의 원리를 벗어나진 않지만 구현에서 살짝 다른 부분이 있습니다.
아래의 코드에서 bfs 메서드를 자세히 보겠습니다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main_BFS_Grid {
static int row, col;
static int matrix[][];
static boolean visit[][];
// 4방향으로 탐색하기 위한 x와 y의 delta 값
static int dx[] = {1, -1, 0, 0};
static int dy[] = {0, 0, 1, -1};
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 2차원 격자의 높이, 너비 저장
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
row = Integer.parseInt(st.nextToken());
col = Integer.parseInt(st.nextToken());
// 2차원 배열 및 방문 배열 초기화
// 2차원 배열이므로 방문 배열도 2차원 형태로 선언
matrix = new int[row][col];
visit = new boolean[row][col];
// 2차원 배열 저장
for(int i = 0; i < row; i++) {
st = new StringTokenizer(br.readLine(), " ");
for(int j = 0; j < col; j++) {
matrix[i][j] = Integer.parseInt(st.nextToken());
}
}
// 탐색을 시작할 위치와 목표 위치 저장
st = new StringTokenizer(br.readLine(), " ");
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
// 탐색 시작
int result = bfs(x1, y1, x2, y2);
// 출력
System.out.println(result);
}
private static int bfs(int x1, int y1, int x2, int y2) {
Queue<int[]> q = new ArrayDeque<>();
// 노드의 위치가 2차원 좌표로 저장되어있기 때문에 x 좌표, y 좌표, 거리 순으로 저장해야 함
q.offer(new int[] {x1, y1, 0});
visit[x1][y1] = true;
while(!q.isEmpty()) { // 큐가 빌 때까지 반복
// 큐에 있는 노드 추출
int[] poll = q.poll();
// 목표에 도달한 경우 거리 반환
if(poll[0] == x2 && poll[1] == y2) {
return poll[2]; // 3번째 위치에 있음을 주의
}
// 현재 노드의 위치에서 4 방향으로 탐색하면서 좌표값 계싼
for(int delta = 0; delta < 4; delta++) {
int nx = poll[0] + dx[delta];
int ny = poll[1] + dy[delta];
// 상하좌우로 새로 이동한 좌표가 2차원 배열의 범위를 벗어나는 지 체크하고
// 방문한 적이 있는 지 체크
if(nx >= 0 && nx < row && ny >= 0 && ny < col && !visit[nx][ny]) {
// 방문한 적이 없는 노드의 위치에 대해 큐에 추가
// 거리는 현재 노드까지 오는 거리+1 값
q.offer(new int[] {nx, ny, poll[2]+1});
// 방문 처리
visit[nx][ny] = true;
}
}
}
// 도달하지 못한 경우
return -1;
}
}입력
5 5
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 3 4
출력
7
인접한 노드를 탐색할 때 dx와 dy를 이용해 4가지 방향으로 조회하는 것을 볼 수 있습니다. delta 값이 0부터 3까지 증가하면서 하→상 → 우 → 좌 순으로 탐색합니다. 그리고 새로 접근한 노드가 좌표를 벗어나는 지 체크해서 ArrayIndexOutOfBoundException을 예방합니다.
이 BFS 코드는 무궁무진하게 응용이 가능합니다. 대표적으로 몇 가지 살펴보자면
1. 탐색 방향 커스텀
체스 문제에서 나이트는 상하좌우가 아니라 아래의 그림처럼 이동합니다.

이때 나이트가 특정 위치로 이동하는 최단 거리를 알고 싶을 때 방향을 어떻게 설정 해야할까요?
// 8방향으로 탐색하기 위한 x와 y의 delta 값
static int dx[] = {-2, -1, 1, 2, 2, 1, -1, -2};
static int dy[] = {1, 2, 2, 1, -1, -2, -2, -1};
// 현재 노드의 위치에서 8 방향으로 탐색하면서 좌표값 계싼
for(int delta = 0; delta < 8; delta++) {
int nx = poll[0] + dx[delta];
int ny = poll[1] + dy[delta];
if(nx >= 0 && nx < row && ny >= 0 && ny < col && !visit[nx][ny]) {
q.offer(new int[] {nx, ny, poll[2]+1});
visit[nx][ny] = true;
}
}
dx와 dy를 나이트의 이동방향에 맞게 수정한 뒤에 BFS 동작 시 delta 값을 8까지 늘리면 원하는 방향으로 이동할 수 있게 됩니다.
2. 그리드에 장애물이 존재하는 경우
사실 2차원 격자 그래프가 전부 0으로만 채워진 경우에 대한 문제는 굳이 출제하지 않습니다. 2차원 격자 그래프는 주로 격자 내에 장애물이 존재하거나 원하는 위치로만 이동해야할 때 최단 거리를 구하기 위해 사용합니다.
아래의 경우를 보겠습니다.

0이 이동할 수 있는 노드고, 1은 벽이라서 이동할 수 없다고 하겠습니다. 이때 0, 0에서 너비 우선 탐색을 시작하면 전처럼 7이 출력되는 것이 아니라 15가 출력됩니다.
이런 경우 BFS를 아래처럼 수정하면 됩니다.
for(int delta = 0; delta < 4; delta++) {
int nx = poll[0] + dx[delta];
int ny = poll[1] + dy[delta];
// 조건에 matrix[nx][ny] == 0을 추가
if(nx >= 0 && nx < row && ny >= 0 && ny < col && !visit[nx][ny] && matrix[nx][ny] == 0) {
q.offer(new int[] {nx, ny, poll[2]+1});
visit[nx][ny] = true;
}
}
matrix[nx][ny] == 0을 AND 조건으로 추가했기 때문에 벽이 존재하는 노드는 큐에 추가하지 않습니다.
3. 덩어리 개수 세기
2번의 경우에서 봤던 2차원 격자 그래프에서 1을 벽이 아니라 땅, 0을 바다로 정의하겠습니다. 이때 섬의 개수를 구하는 문제도 흔히 출제되는 BFS 문제입니다.
이땐 아래처럼 bfs 메서드를 호출할 때마다 cnt를 증가시키며 카운트하면 됩니다.
for(int i = 0; i < row; i++) {
for(int j = 0; j < col; j++) {
if(!visit[i][j] && matrix[i][j] == 1) { // 방문하지 않은 경우 탐색 시작
bfs(i, j);
cnt++;
}
}
}
.
.
.
마치며
BFS는 그래프 탐색 알고리즘 중 가장 기본적으로 알아야 할 알고리즘이지만 마냥 쉽지는 않습니다. 알고리즘 공부하고 백준에서 꼭 문제 풀어보셨으면 좋겠습니다.
아래는 BFS를 처음 접하고 풀기 좋은 문제들입니다.
- 2606 바이러스 : https://www.acmicpc.net/problem/2606
- 2178 미로 탐색 : https://www.acmicpc.net/problem/2178
- 7576 토마토 : https://www.acmicpc.net/problem/7576
- 2206 벽 부수고 이동하기 : https://www.acmicpc.net/problem/2206
난이도 순으로 작성했으나 난이도의 갭이 크기 때문에 문제를 풀었더라도 비슷한 난이도의 문제를 더 도전하고 다음 문제를 풀어보면 좋을 것 같습니다.
궁금한 점이나 피드백은 댓글로 부탁드립니다. 😊
'Algorithm > Graph' 카테고리의 다른 글
| [Algorithm] Bellman-Ford 알고리즘 with JAVA (0) | 2025.05.19 |
|---|---|
| [Algorithm] 0-1 BFS 알고리즘 with JAVA (1) | 2025.05.15 |
| [Algorithm] Dijkstra 알고리즘 with JAVA (0) | 2025.05.12 |
| [Algorithm] 그래프 이론 및 그래프 탐색 (1) | 2025.05.09 |
| [Algorithm] Floyd-Warshall 알고리즘 with JAVA (0) | 2025.04.26 |