
들어가며
길이가 100만인 배열에서 특정 구간의 합을 구하는 것은 for문을 사용해서 쉽게 구할 수 있습니다. 하지만 구해야하는 특정 구간이 한 번이 아니라 10만 번인 경우엔 어떻게 구할까요? 이번 글에서 알아볼 알고리즘은 누적합이라는 알고리즘입니다.
누적합: Prefix Sum
1. 개요
배열에서 특정 구간의 합을 반복적으로 구해야 하는 문제가 코딩 테스트에서 자주 등장합니다. 단순하게 매번 특정 구간을 순회하면 시간이 너무 오래걸리기 때문에 이를 개선하기 위해 누적합 기법이 고안되었습니다.
누적합은 한 번의 배열 전체 순회를 통해 배열의 합 정보를 저장해두고, 이후 각각의 구간합 요청에 대해 빠르게 응답할 수 있습니다.
2. 시간복잡도
원본 배열의 길이가 N일 때, 인덱스 0부터 N-1까지 한번씩의 연산이 발생하므로 시간복잡도는 O(N)입니다.
만약, 누적합을 사용하지 않으면 시간복잡도는 최악의 경우 O(N*N)입니다.
3. 성격
누적합 알고리즘은 아래와 같은 성격을 가지는 알고리즘입니다.
- 전처리(Preprocessing) : 본격적인 문제 풀이 전에 미리 계산해두기 때문
- 동적 계획법(Dynamic Programming) : 작은 문제의 답을 구해서 더 큰 문제를 구하기 때문
- 쿼리 최적화(Query Optimization) : 반복적으로 들어오는 질의에 대해 빠르게 응답하기 때문
4. 동작 방식
- 기본적으로 원본 배열과 누적된 합을 저장할 배열을 하나 따로 만듭니다.
- 원본 배열에 원소를 전부 입력 받습니다.
- 누적합 배열의 두번째 인덱스부터 이전 누적합 배열의 값 + 원본 배열의 현재 인덱스값을 할당합니다.
이렇게 누적합 배열을 전부 완성했으면 각각의 쿼리에 대해 구간의 합을 구할 수 있습니다. 자세한 설명은 아래의 그림과 함께 보겠습니다. (참고로 이번 글에서 나오는 모든 배열의 예시들은 엑셀 난수로 생성했습니다)
그림으로 보는 누적합 구하기

길이가 10인 int형 배열을 예시로 설명하겠습니다. 여기서 등장하는 origin 배열과 아래의 sum 배열은 1-based array입니다. 계산 편의를 위해 1번 인덱스부터 유효한 숫자를 저장했습니다.
위의 origin 배열의 누적합을 계산하면 아래와 같습니다.

화살표를 따라가보면 쉽게 이해할 수 있습니다. sum의 이전 인덱스 값과 현재 origin 값을 더해서 현재의 sum 인덱스에 할당하는 방식입니다.
sum 배열의 각각의 인덱스는 1번 인덱스부터 현재 인덱스까지의 합을 의미합니다.
이렇게 누적합 배열을 완성했습니다. 그러면 이 누적합 배열을 어떻게 활용해야할지 알아보도록 하겠습니다.
누적합 배열 활용
누적합 알고리즘을 활용하는 가장 단순한 요구사항은 배열의 특정 구간의 합을 구하는 문제입니다. 따라서 특정 구간의 쿼리를 처리할 수 있도록 누적합 배열을 구했습니다.

앞선 예시를 다시 가져왔습니다.
여기서 sum 배열의 각각의 값은 첫번째 원소부터 현재 원소까지의 합입니다. 예를 들어, sum[4] = 6+3+2+1 = 12로 첫번째 원소부터 현재 원소까지의 합인 것을 알 수 있습니다.
여기서 우리가 궁금한 것은 i번째 인덱스부터 j번째 인덱스까지의 합입니다.
i와 j를 아래처럼 가정하고 흐름을 따라가보도록 하겠습니다.
i) i = 4, j = 7
$\large \sum_{1}^{4} origin_i = 6+3+2+1 = 12$
1부터 4까지의 합은 12입니다.
$\large \sum_{1}^{7} origin_i = 6+3+2+1+7+3+4 = 26$
또한 1부터 7까지의 합은 26입니다.
$\large \sum_{4}^{7} origin_i = 1+7+3+4 = 15$
마지막으로 우리가 구하려는 4부터 7까지의 합을 직접 구해보면 15가 나옵니다.
이 값은 sum[7] - sum[4-1]의 값과 일치합니다.
여기서 뭔가 감이 잡히나요? 다른 예시를 하나 더 보겠습니다.
i) i = 6, j = 10
$\large \sum_{1}^{6} origin_i = 6+3+2+1+7+3 = 22$
1부터 6까지의 합은 22입니다.
$\large \sum_{1}^{10} origin_i = 6+3+2+1+7+3+4+3+8+2 = 39$
또한 1부터 10까지의 합은 39입니다.
$\large \sum_{6}^{10} origin_i = 3+4+3+8+2 = 20$
마지막으로 우리가 구하려는 6부터 10까지의 합을 직접 구해보면 20이 나옵니다.
이 값은 sum[10] - sum[6-1]의 값과 일치합니다.
일반화해보면 i부터 j까지의 합은 sum[j] - sum[i-1]인 것을 알 수 있습니다.
두번째 항이 sum[i]가 아니라 sum[i-1]인 이유?
인덱스 i에 대해 sum[i]의 값은 1부터 i까지의 합입니다. 즉, i번째 인덱스의 값까지 더해진 값이라는 뜻입니다.
따라서 만약 sum[i]를 빼버리면 i부터 j까지의 합에서 origin[j]의 값을 뺀 i+1부터 j까지의 합과 같게 됩니다. 따라서 i를 포함하려면 두번째 항은 sum[i-1]이 되어야합니다.
이제 누적합 알고리즘을 자바 코드로 어떻게 구현하는지 자세히 알아보겠습니다.
자바 코드로 구현한 누적합 알고리즘
1. 누적합 구하기
여기서부턴 코드 주석에서 자세히 설명하겠습니다.
package PrefixSum;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main_PrefixSum {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int n = Integer.parseInt(st.nextToken()); // 배열의 원소 개수
int query = Integer.parseInt(st.nextToken()); // 쿼리 개수
int[] origin = new int[n+1]; // 원본 배열
int[] sum = new int[n+1]; // 누적합 배열
// 원본 배열 입력
st = new StringTokenizer(br.readLine(), " ");
for(int i = 1; i <= n; i++) {
origin[i] = Integer.parseInt(st.nextToken());
}
// 누적합 배열 계산
for(int i = 1; i <= n; i++) {
// 이전 인덱스인 i-1과 현재의 원소인 origin[i]를 더해서 할당
sum[i] = sum[i-1] + origin[i];
}
// 누적합 배열 출력
System.out.println(Arrays.toString(sum));
}
}입력
10 10
6 3 2 1 7 3 4 3 8 2
출력
[0, 6, 9, 11, 12, 19, 22, 26, 29, 37, 39]
TIP!
쿼리에서 원본 배열을 필요로하지 않는다면 굳이 sum 배열을 만들지 않고 origin 배열에 덮어쓰는 것도 가능합니다. 그러면 누적합 배열은 origin[i] += origin[i-1]와 같이 구하면 됩니다.
sum 배열을 생성하지 않으면 메모리와 시간을 많이 절감할 수 있습니다.
2. 쿼리 처리
누적합 배열을 만들었으면 이젠 활용해야합니다. 일반적으로 쿼리는 A B의 형태로 주어집니다. A번째 원소부터 B번째 원소까지의 합을 묻는 쿼리입니다.
StringBuilder sb = new StringBuilder();
for(int i = 0; i < query; i++) {
st = new StringTokenizer(br.readLine(), " ");
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
sb.append(sum[end]-sum[start-1]+"\n");
}
System.out.println(sb.toString().trim());입력
10 5
6 3 2 1 7 3 4 3 8 2
2 7
5 10
3 7
5 5
1 10
출력
20
27
17
7
39
위에서 설명했던 예제를 입력했기 때문에 표와 출력값을 비교하면 일치하는 것을 알 수 있습니다.
2차원 배열의 누적합
지금까지 1차원 배열에 대해 누적합 배열을 만들어서 쿼리를 빠르게 처리했습니다. 2차원 배열에 대해서도 비슷하게 누적합 배열을 만들어서 빠르게 쿼리를 처리할 수 있습니다.
먼저 아까처럼 그림으로 이해를 돕기 위해 예시 2차원 배열을 가져왔습니다.

2차원 누적합을 구하는 과정은 크게 2가지로 분류할 수 있습니다.
- 왼쪽 또는 위쪽 원소의 값이 0인 경우(1-based array의 2번째 행 또는 2번째 열)
- 그렇지 않은 경우(나머지)
1. 위쪽 또는 위쪽 원소의 값이 0인 경우

먼저 왼쪽 또는 위쪽 원소의 값이 0인 경우입니다. 이 경우엔 그냥 1차원 배열의 누적합을 구하는 것과 다를 바가 없습니다. 행과 열 모두 같은 원리이므로 2번째 행(10, 4, 8, 12, 10)을 기준으로 설명해보겠습니다.
2차원 누적합에서 sum[i][j]는 origin[1][1]에서 origin[i][j]에 있는 원소들의 합$$=\sum_{x=1}^{i}\sum_{y=1}^{j} origin_{(x,\ y)}$$을 뜻합니다. 2번째 행에서 각각의 원소들의 위에는 아무 원소도 없기 때문에 왼쪽의 원소에 의해서만 값이 누적됩니다.
따라서 아래처럼 2차원 누적합 배열을 완성시킬 수 있습니다. (origin과 sum배열 모두 2차원이라 따로 누적합 그림을 만들었습니다.)
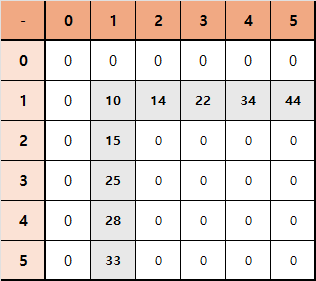
2. 그렇지 않은 경우(나머지)
이제 남은 건 sum[2][2]부터 sum[5][5]까지입니다. 처음 보면 이해가 어려울 수 있어 아래의 예시와 함께 천천히 따라가보겠습니다.
i) (i, j) = (2, 2)
sum[2][2]를 구하는 방법입니다.

단순하게 생각해보면 (2, 2)의 위와 왼쪽 항을 더하면 얼추 누적합의 모양새가 나옵니다. 한 번 더해보겠습니다.
$sum[1][2]+sum[2][1] = 14+15 = 29$이고 원본 배열의 origin[2][2]까지 더해주면 $29+origin[2][2] = 32$이므로 우리가 실제로 구해야하는 값인 $10+5+4+3=22$보다 10이나 큽니다. 이유가 뭘까요?
우리가 계산한 값을 뜯어서 보겠습니다.
$sum[1][2] = 10 + 4 = 14$
$sum[2][1] = 10 + 5 = 15$
$sum[2][2] = 10 + 4 + 10 + 5 + 3 = 32$
실제로 나와야하는 값보다 우리가 구한 값이 더 컸던 이유는 (2, 2)의 왼쪽 상단 원소가 한 번 더 더해졌기 때문이었습니다. 따라서 우리가 구한 값에서 왼쪽 상단의 원소를 한 번 빼면 정확한 누적합 값을 구할 수 있습니다.
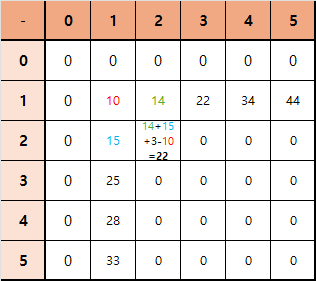
위의 예시를 통해 점화식을 구할 수 있습니다.
$$sum[i][j] = sum[i-1][j] + sum[i][j-1] + origin[i][j] - sum[i-1][j-1]$$
이것을 이용해서 나머지 원소들에도 확장할 수 있습니다.

Q. 점화식에서 sum[i-1][j-1]이 아니라 origin[i-1][j-1]을 빼야하는거 아닌가요?
A. 그렇지 않습니다! 뺄셈이 필요한 이유가 sum[i][j-1]과 sum[i-1][j]를 더하면서 중복된 부분을 빼주려고 하는 것인데 중복된 부분은 sum[i-1][j-1]이지 origin[i-1][j-1]이 아니기 때문입니다.
2차원 배열의 누적합의 활용
2차원 배열에서도 누적합을 활용하는 방법을 알아보겠습니다. 1차원의 경우와 마찬가지로 예시를 들어서 설명한 뒤 일반화해보겠습니다.
i) (3, 2) → (5, 4)
(3, 2)에서 (5, 4)까지 9개의 셀의 합을 구하는 쿼리입니다.

그리고 아래는 (3, 2)부터 (5, 4)까지의 합을 구하는 그림인데 각각의 사각형이 집합이라고 생각하면 이해가 더 쉽습니다.

위의 그림을 수식으로 나타내면 $sum[3 to 5][2 to 4] = sum[5][4] - sum[5][1] - sum[2][4] + sum[2][1]$입니다. 말로 쉽게 설명하면 전체에서 짜투리를 잘라내고 두 번 잘라낸 짜투리는 다시 더해주는 방식입니다.
이걸 점화식으로 작성하면 $$\sum_{i=sx}^{ex}\sum_{j=sy}^{ey} origin_{(i, j)}= sum[ex][ey] - sum[sx-1][ey] - sum[ex][sy-1] + sum[sx-1][sy-1]$$
여기서 (sx, sy)는 시작점이고, (ex, ey)는 종점입니다.
자바 코드로 구현한 2차원 배열의 누적합
1차원 배열의 누적합 자바 코드를 이해했다면 2차원 배열의 누적합 코드도 금방 이해될 것이라 생각해 주석은 간단하게 적었습니다.
1. 누적합 구하기
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main_PrefixSum_2D {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 2차원 배열의 가로, 세로 길이 입력
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int row = Integer.parseInt(st.nextToken());
int col = Integer.parseInt(st.nextToken());
// 원본 배열 초기화
int[][] origin = new int[row+1][col+1];
// 원본 배열 입력
for(int i = 1; i <= row; i++) {
st = new StringTokenizer(br.readLine(), " ");
for(int j = 1; j <= col; j++) {
origin[i][j] = Integer.parseInt(st.nextToken());
}
}
// 누적합 배열 초기화
int[][] sum = new int[row+1][col+1];
// 누적합 배열 점화식으로 계산
for(int i = 1; i <= row; i++) {
for(int j = 1; j <= col; j++) {
sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + origin[i][j];
}
}
// 출력
StringBuilder sb = new StringBuilder();
for(int i = 1; i <= row; i++) {
for(int j = 1; j <= col; j++) {
sb.append(sum[i][j]+" ");
}
sb.append("\n");
}
System.out.println(sb.toString().trim());
}
}입력
5 5
10 4 8 12 10
5 3 11 4 6
10 6 13 1 15
3 13 12 15 7
5 10 9 7 14
출력
10 14 22 34 44
15 22 41 57 73
25 38 70 87,118
28 54 98 130 168
33 69 122 161 213
2. 쿼리 처리
// 쿼리 개수
int query = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
for(int idx = 0; idx < query; idx++) {
// 시작지점 ~ 종료지점 입력
st = new StringTokenizer(br.readLine(), " ");
int sx = Integer.parseInt(st.nextToken());
int sy = Integer.parseInt(st.nextToken());
int ex = Integer.parseInt(st.nextToken());
int ey = Integer.parseInt(st.nextToken());
// 2차원 배열에서 누적합은 앞서 설명한 것과 동일한 수식
int answer = sum[ex][ey] - sum[sx - 1][ey] - sum[ex][sy - 1] + sum[sx - 1][sy - 1];
sb.append(answer+"\n");
}
// 출력
System.out.println(sb.toString().trim());입력
5 5
10 4 8 12 10
5 3 11 4 6
10 6 13 1 15
3 13 12 15 7
5 10 9 7 14
5
1 1 5 5
1 1 1 1
2 2 4 5
3 1 5 1
5 1 5 5
출력
213
10
106
18
45
.
.
.
마치며
마지막으로 누적합을 연습하기 좋은 문제들 아래에 추천드립니다!
- 11659번 구간 합 구하기4 : https://www.acmicpc.net/problem/11659
- 2167번 2차원 배열의 합 : https://www.acmicpc.net/problem/2167
- 11660 구간 합 구하기5 : https://www.acmicpc.net/problem/11660
- 15724번 주지수 : https://www.acmicpc.net/problem/15724
첫번째 문제는 1차원 배열의 누적합을 연습하는 문제, 두번째는 1차원 배열의 누적합을 응용하는 문제, 마지막 두 문제는 2차원 배열의 누적합 문제입니다.
누적합 알고리즘이 사실 알고리즘의 기본에 속하는데 설명하려니까 되게 장황해졌네요. 바쁜 일이 있어서 거의 2달 만에 글을 썼는데 다시 열심히 써보겠습니다!
궁금한 점이나 피드백은 댓글로 부탁드립니다! 😊
'Algorithm' 카테고리의 다른 글
| [Algorithm] IMOS 기법: 누적합과 차분 배열로 빠른 구간 업데이트 with Java (0) | 2026.01.27 |
|---|---|
| [Algorithm] 분할 정복을 이용한 행렬의 거듭제곱으로 Fibonacci 수열 구하기 with JAVA (0) | 2025.01.07 |