들어가며
프로그래밍 언어로 피보나치 수를 구하는 방법은 크게 3가지 있습니다. 재귀와 동적 프로그래밍을 통해 피보나치 수를 구하는 것은 우리가 익히 알고 있습니다. 재귀 방식을 사용하면 하나의 호출이 2개의 호출을 발생시키므로 시간 복잡도가 O(2^n)으로 높은 시간복잡도를 요구합니다. 하지만, 동적 프로그래밍 방식(이하 DP)으로 메모이제이션을 사용한다면 시간 복잡도 O(n)으로 획기적으로 시간을 줄일 수 있습니다.
재귀 방식에선 일반적으로 30~40번째 피보나치 수를 구할 수 있고, DP 방식에선 시간 복잡도에 따라 100만에서 1000만까지 가능하지만 long의 범위를 한참 벗어나고, 메모리 초과가 발생하기 때문에 현실적으로는 BigInteger 타입으로 10만번째 피보나치 수까지 구할 수 있습니다.
하지만 분할 정복을 이용한 거듭제곱으로 피보나치 수를 계산한다면 long 타입의 최댓값인 900경번째의 피보나치 수는 약 60번 이하의 계산으로 구하는 것이 가능합니다. 따라서 1ms도 안되는 시간으로 900경번째 피보나치 수를 구할 수 있습니다. 이 방식은 말 그대로 분할 정복과 행렬의 거듭제곱을 이용해서 피보나치 수를 구하기 때문에 시간 복잡도 O(log n) 밖에 되지 않습니다.
이번 글에선 재귀 호출과 DP 방식을 통해 피보나치 수를 구하는 과정을 간단하게 알아본 뒤에 분할 정복을 이용한 거듭제곱으로 피보나치 수를 구하는 알고리즘을 알아보겠습니다.
재귀 호출
재귀 호출 방식은 앞서 설명했듯이 한 번의 호출이 또 다른 2개의 호출을 발생시킵니다. 계산 값을 따로 저장하지 않고 각 피보나치 순열의 값을 그때그때 계산하기 때문에 시간 복잡도가 n의 제곱으로 아주 큽니다.
아래는 재귀 방식을 통해 40번째 피보나치 수를 구하는 코드입니다.
public class Recursion {
public static void main(String[] args) throws Exception {
long sum = 0;
for(int i = 0; i < 10; i++) {
long start = System.nanoTime();
fibo(40);
long end = System.nanoTime();
sum += (end-start)/1000000;
}
System.out.println(sum/10+"ms");
}
private static int fibo(int n) {
if(n < 1) {
return 0;
} else if(n <= 2) {
return 1;
}
return fibo(n-1)+fibo(n-2);
}
}3회 실행 결과
231ms
241ms
232ms
10번의 계산 후에 평균 시간을 측정해보면 각각 230~240ms가 소요되는 것을 알 수 있습니다. 이때 n이 1씩 커질때마다 시간 복잡도는 기하급수적으로 커지므로 40번째 이후의 피보나치 수를 구하기엔 비효율적입니다.
Dynamic Programming
DP는 재귀 호출과 달리 메모이제이션을 사용합니다. 즉, 이전에 계산했던 피보나치 순열을 이용해서 다음 피보나치 수를 구하기 때문에 재귀 방식보다 월등히 빠릅니다.
아래는 DP 방식을 통해 10만번째 피보나치 수를 구하는 코드입니다.
import java.math.BigInteger;
public class Main_10826_피보나치 {
static BigInteger[] fibo = new BigInteger[100001];
public static void main(String[] args) throws Exception {
long start = System.nanoTime();
fibo[0] = new BigInteger("0");
fibo[1] = new BigInteger("1");
for(int i = 2; i < 100001; i++) {
fibo[i] = fibo[i-1].add(fibo[i-2]);
}
long end = System.nanoTime();
System.out.println((end-start)/1000000+"ms");
}
}3회 실행 결과
342ms
405ms
304ms
DP에서 10만번째 피보나치 수를 구하는 데 걸리는 시간과 재귀 호출에서 40번째 피보나치 수를 구하는 데 걸리는 시간이 비슷한 것을 볼 수 있습니다. BigInteger를 사용했기 때문에 10만번째 이후의 피보나치 수를 구하려면 이제 시간이 아니라 메모리를 관리해야합니다. 따라서 더 큰 피보나치 수를 계산하려면 BigInteger가 아닌 모듈러 연산을 통해 long 타입 범위 이내에서 피보나치 수를 구해야합니다.
아래는 모듈러 연산과 long 타입을 사용해 1000만번째 피보나치 수를 구하는 코드입니다.
public class Main_10826_피보나치 {
static long[] fibo = new long[10000001];
static final int MOD = 1_000_000_007;
public static void main(String[] args) throws Exception {
long start = System.nanoTime();
fibo[0] = 0;
fibo[1] = 1;
for(int i = 2; i < 10000001; i++) {
fibo[i] = (fibo[i-1] + fibo[i-2]) % MOD;
}
long end = System.nanoTime();
System.out.println((end-start)/1000000+"ms");
}
}3회 실행 결과
49ms
32ms
41ms
위에서 1000만번째 피보나치 수를 구하지만 BigInteger가 아닌 원시 타입인 long을 사용하고 모듈러 연산을 사용하기 때문에 메모리 초과가 발생하지도 않고, 소요 시간도 훨씬 적은 것을 알 수 있습니다.
하지만 위의 방식 역시 n이 10억을 넘어서면 4000ms 이상 소요되기 때문에 그 이상의 피보나치 수열을 구하기 위해선 시간이 많이 소요되는 것을 알 수 있습니다.
지금까지 재귀 호출과 DP 방식을 통한 피보나치 수열 계산 방식을 간단하게 훑어봤습니다. 그럼 이젠 분할 정복을 이용한 거듭제곱 방식으로 피보나치 수를 구하는 방법을 자세히 알아보겠습니다.
피보나치 행렬의 거듭제곱
1. 피보나치의 기본 행렬

피보나치 기본 행렬 Q는 위와 같이 정의합니다.
피보나치의 기본 행렬 Q가 위와 같은 이유는 피보나치 수열의 재귀 관계를 정확히 표현할 수 있는 유일한 행렬입니다. 즉, 피보나치 수열의 정의에 기반한 수학적 필연성에 의해 만들어진 것입니다.
피보나치 수열은 F(n) = F(n-1) + F(n-2) 인데 위의 피보나치 기본 행렬인 Q에 자기 자신인 Q를 하나씩 곱할때마다 피보나치 수열의 값과 동일한 값이 나오는 것을 볼 수 있습니다. 즉, Q의 점화식은 아래와 같습니다.
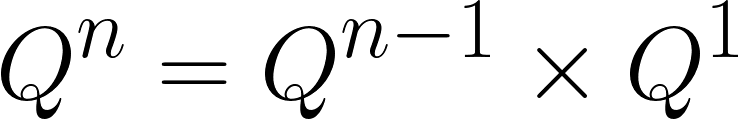
또한, 행렬 Q의 n차수는 Q가 n번 곱해졌다는 의미이므로 아래와 같이 일반화도 가능합니다.

말로만 이해하려면 어렵기 때문에 아래의 피보나치 행렬 Q의 차수를 1씩 증가시키면서 값을 확인해보겠습니다.
i) n = 1

n = 1일 때는 피보나치 기본 행렬과 동일합니다.
ii) n = 2
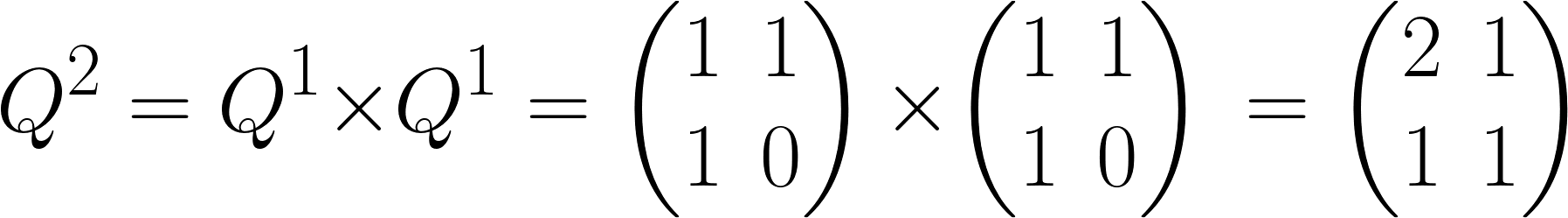
n = 2인 경우 Q가 2번 곱해졌기 때문에 위와 같습니다.
iii) n = 3
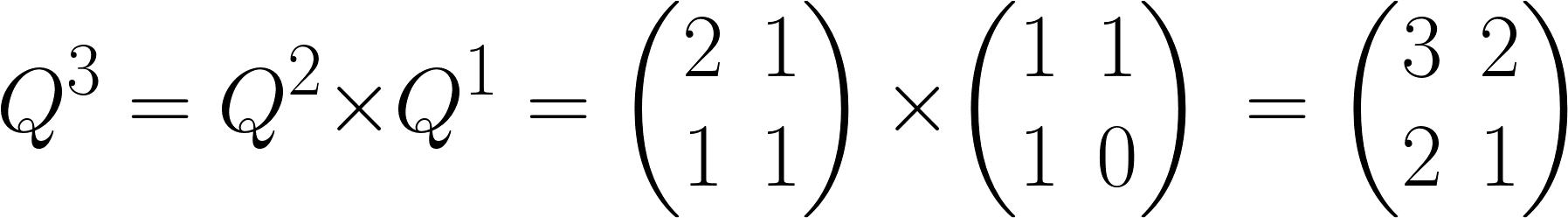
n = 3인 경우 Q의 2번째 행렬에 Q를 한 번 더 곱했기 때문에 위와 같습니다.
iv) n = 4

n = 4인 경우도 마찬가지로 위와 같이 계산할 수 있습니다.
v) n = 5

마지막으로, n = 5인 경우도 위와 같이 구했습니다.
TIP. 다시 강조!
피보나치 기본 행렬이 위의 사진과 같은 경우에만 행렬을 계속 곱했을 때 피보나치 수를 거듭제곱으로 알아낼 수 있기 때문에 피보나치의 기본 행렬을 (1 1 1 0)으로 정의했습니다.
2. 피보나치 행렬과 피보나치 수열의 관계
직전에 피보나치 행렬의 차수를 1씩 증가시키면서 값을 계산해봤습니다. 그리고 위의 행렬의 값들을 유심히 살펴보면 각각의 성분들은 모두 피보나치 수열에서 등장하는 숫자임을 알 수 있습니다.
이 점을 이용해서 피보나치 행렬과 피보나치 수열의 관계를 아래처럼 나타낼 수 있습니다.

즉, 피보나치 행렬을 n-1번 곱하면 피보나치 수열의 n번째 값을 알아낼 수 있습니다. 다시 말해서 F(n)의 갑슬 구하려면 피보나치 행렬의 n-1번째 행렬을 구하면 됩니다.
위의 식을 통해서 1000만번째 피보나치 수를 구해보면 실행 시간은 DP와 비슷합니다. 그 이유는 DP에서와 마찬가지로 메모이제이션으로 이전 행렬에 계속 기본 행렬을 곱해나가는 방식이기 때문입니다.
하지만 피보나치 행렬 방식은 DP와 가장 큰 차이점이 있습니다. DP는 덧셈 연산이지만 피보나치 행렬은 계속 곱해나간다는 점입니다. 분할 정복을 이용하면 훨씬 빠르게 F(n) 값에 도달할 수 있습니다.
분할 정복을 이용한 피보나치 행렬의 거듭제곱
1. 분할 정복을 하는 이유
피보나치 수열 F(n)을 구하려면 n-1과 n-2 항의 값을 더하기 때문에 n번째 피보나치 수열을 구하기까지 총 n번의 연산이 필요합니다.
마찬가지로 피보나치 행렬 Q에 자기자신 Q를 계속 곱해나가며 n번째 피보나치 행렬을 구하려면 총 n번의 곱셈 연산이 필요합니다. 이는 DP 방식과 다를 게 없습니다.
하지만 n의 절반인 n/2를 알고 있다면 행렬 Q^n/2와 Q^n/2를 곱해서 Q^n을 구할 수 있습니다. 이렇게 n의 값을 반으로 쪼개고 쪼갠다면 약 log n번의 연산으로 n번째 피보나치 행렬의 값을 구할 수 있게 됩니다.
n = 16인 경우, 아래의 그림을 통해 실제로 연산이 얼마나 단축되는지 확인하겠습니다.
i) 단순 곱셈 방식
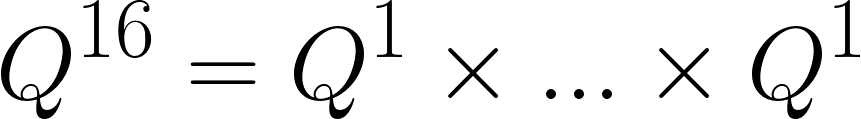
피보나치 기본 행렬 Q를 16번 곱하기 때문에 연산량은 총 16입니다.
ii) 분할 정복 방식
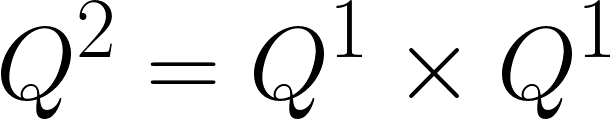
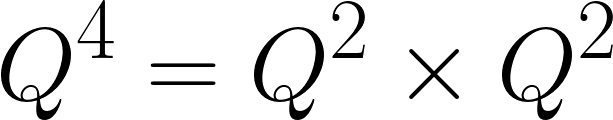
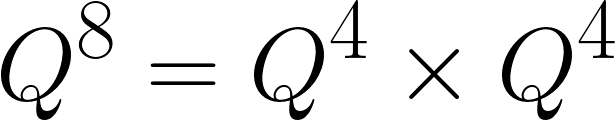

n = 1부터 거듭제곱 방식으로 구하기 때문에 n = 3, 5, 6, 7 등의 연산에 대해 건너뛸 수 있습니다. 따라서 총 연산 횟수는 4번으로 시간 복잡도 O(log n)을 따르는 것을 알 수 있습니다.
이렇듯 분할 정복으로 행렬을 거듭제곱하면 구하려는 n이 얼마나 큰지에 관계없이 빠르게 구할 수 있습니다. n의 값이 long 타입의 최댓값인 900경인 경우에도 대략 60번 이하의 연산으로 피보나치 수를 구할 수 있습니다.
2. 분할 정복 곱셈 규칙
분할 정복 알고리즘의 정의는 큰 문제를 잘게 쪼개서 작은 문제부터 해결해나가는 방식입니다. 따라서 직전에 n = 16인 경우에도 16을 쪼개서 8로, 8을 쪼개서 4로, 4를 쪼개서 2로, 2를 쪼개서 1을 만든 뒤에 1부터 차례대로 곱해서 16번째 행렬을 구하는 방식으로 코드를 구현해야합니다.
위에서 n이 짝수인 경우에 대해서 2로 나누어 분할 정복 연산을 한다는 것을 확인했습니다. 그렇다면 n이 홀수인 경우 어떻게 작은 문제로 나눠야하는지 알아보겠습니다.
i) 홀수를 n/2와 n/2+1로 나눔
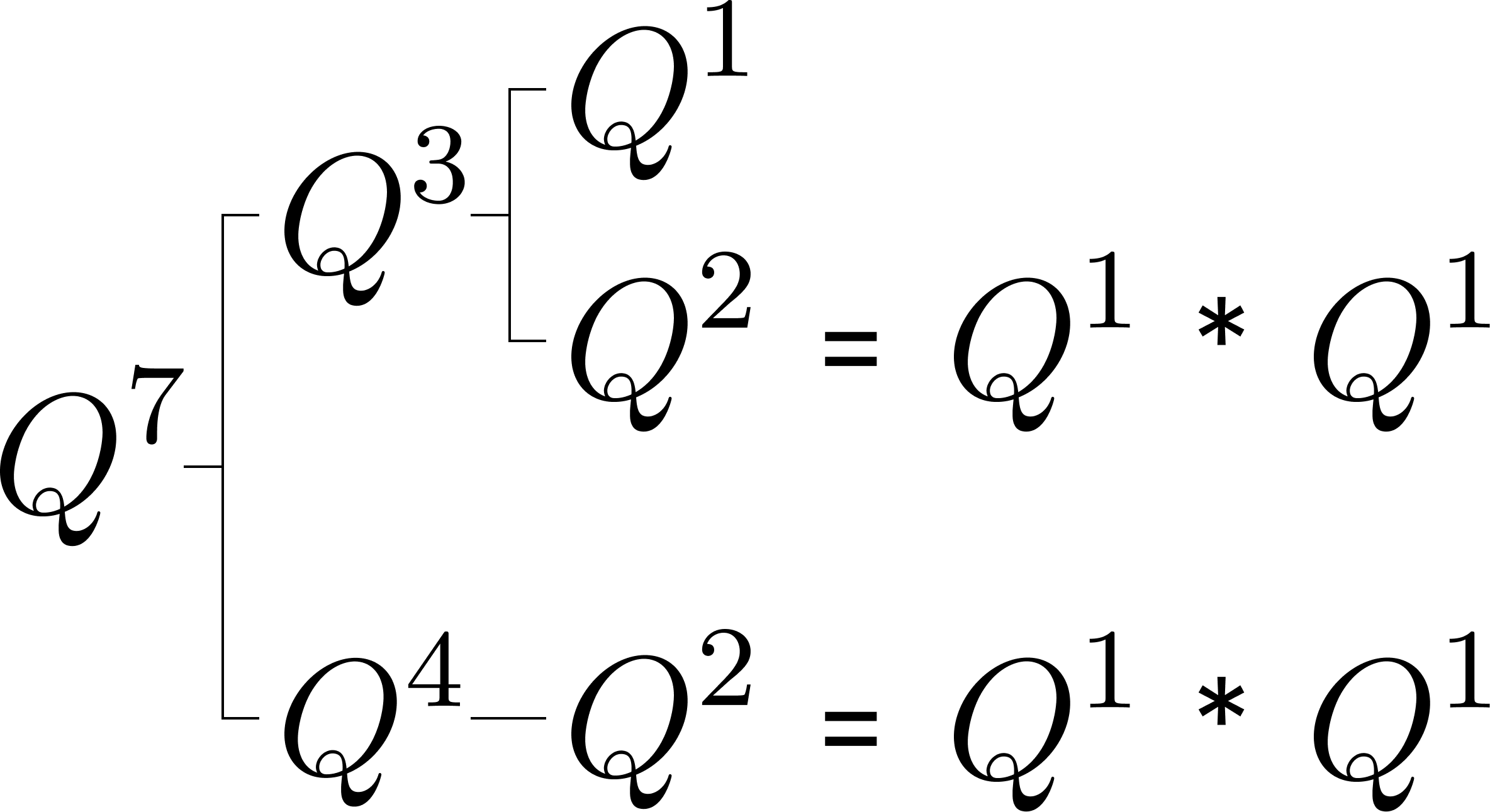
n = 7인 경우 위의 그림을 통해 홀수를 절반으로 나누는 구현을 시각적으로 나타냈습니다. 만약 7을 3과 4로 나눈다면 각각의 재귀 호출은 독립적이기 때문에 Q^2를 따로 구해줘야합니다. 만약, n이 7보다 훨씬 커진다면 중복 연산 횟수도 훨씬 많아지게 됩니다.
ii) 홀수를 1과 n-1로 나눔
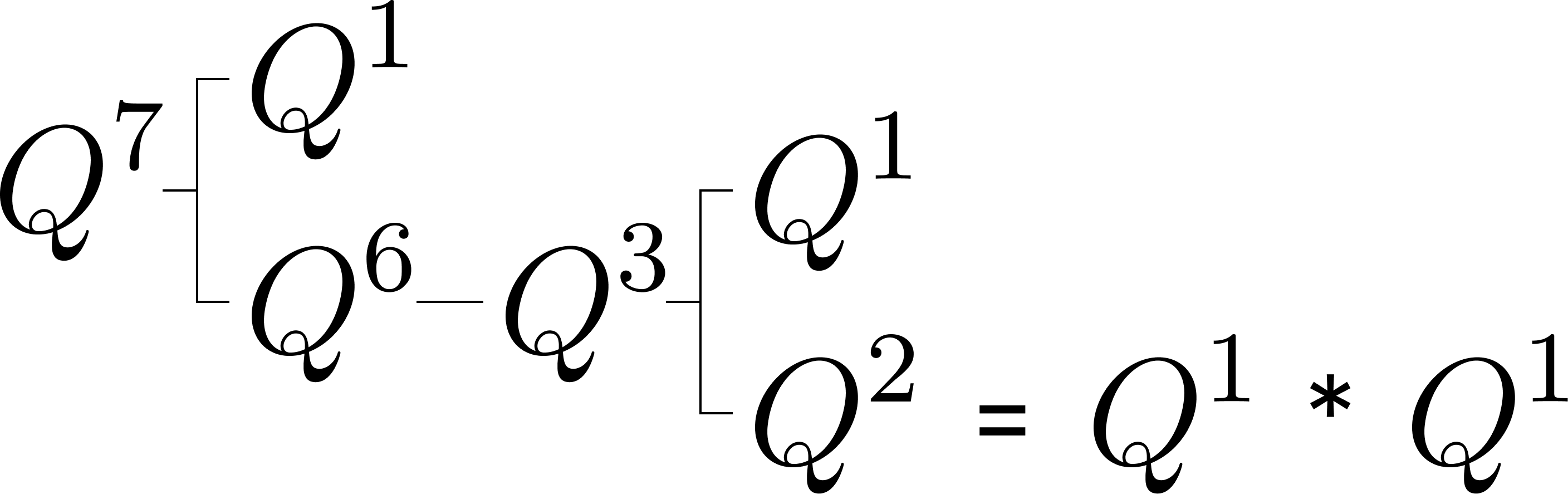
하지만 홀수인 경우 n을 1과 n-1로 분리한다면 위와 같이 중복된 연산 없이 피보나치 수를 구할 수 있음을 확인할 수 있습니다.
따라서 재귀호출의 규칙은 아래와 같이 정리할 수 있습니다.

이제 실제 분할 정복을 이용해 피보나치 행렬을 구하고 피보나치 수를 구하는 코드를 보겠습니다.
분할 정복을 이용한 거듭제곱 구현 코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
public class Fibonacci {
static final int MOD = 1000000007;
static long[][] origin = {
{1, 1},
{1, 0}
};
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
long n = Long.parseLong(br.readLine());
System.out.println(fibo(n));
}
public static long fibo(long n) {
if (n == 0) return 0;
if (n == 1) return 1;
long[][] result = power(origin, n-1);
return result[0][0];
}
private static long[][] power(long[][] matrix, long n) {
if (n == 0) {
return new long[][] {{1,0},{0,1}};
}
if (n == 1) {
return matrix;
}
if (n % 2 == 0) {
long[][] half = power(matrix, n/2);
return multiple(half, half);
} else {
return multiple(matrix, power(matrix, n-1));
}
}
public static long[][] multiple(long[][] A, long[][] B){
long[][] multi = new long[2][2];
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
for (int k = 0; k < 2; k++) {
multi[i][j] += A[i][k] * B[k][j];
multi[i][j] %= MOD;
}
}
}
return multi;
}
}
1. 멤버 변수
- MOD : 모듈러 연산을 위한 변수로 오버플로우 및 메모리 초과 방지
- origin 배열 : 피보나치 기본 행렬로 Q^1에 해당
모듈러 연산이 모르는 분들은 아래 글을 참고 바랍니다!
추가 예정!
2. multiple 메서드
public static long[][] multiple(long[][] A, long[][] B){
long[][] multi = new long[2][2];
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
for (int k = 0; k < 2; k++) {
multi[i][j] += A[i][k] * B[k][j];
multi[i][j] %= MOD;
}
}
}
return multi;
}
multiple 메서드는 두 행렬의 곱셈 결과를 반환하는 단순 연산 메서드입니다. 가장 작은 영역부터 차례로 두 행렬을 곱한 뒤 곱해진 피보나치 행렬을 반환합니다.
오버플로우를 막기 위해 곱셈 과정에서 모듈러 연산이 필요합니다.
3. power 메서드
private static long[][] power(long[][] matrix, long n) {
if (n == 0) {
return new long[][] {{1,0},{0,1}};
}
if (n == 1) {
return matrix;
}
if (n % 2 == 0) {
long[][] half = power(matrix, n/2);
return multiple(half, half);
} else {
return multiple(matrix, power(matrix, n-1));
}
}
power 메서드는 행렬의 거듭제곱을 분할 정복 방식으로 계산하는 메서드입니다. 기저조건과 재귀 호출을 가지고 있어, 피보나치 행렬 Q를 n-1번 곱해 F(n)을 구하는 기능을 합니다.
i) n = 1
n = 1인 경우 더이상 곱셈 연산이 필요없기 때문에 자기 자신을 반환하며 종료합니다.
ii) n = 0
n = 0인 경우는 피보나치 수열의 첫번째. 즉, 피보나치 행렬의 0번째 행렬을 뜻합니다. 따라서 n = 0인 경우는 origin 배열이 아닌 단위 행렬을 반환합니다. power를 최초로 호출하는 fibo 메서드에서 n이 0인 경우와 1인 경우에 대해 직접 값을 반환하고 있지만 코드의 안정성을 위해 추가했습니다.
4. fibo 메서드
public static long fibo(long n) {
if (n == 0) return 0;
if (n == 1) return 1;
long[][] result = power(origin, n-1);
return result[0][0];
}
fibo 메서드는 분할 정복을 시작하고 분할 정복을 통해 피보나치 수를 구하는 메서드입니다. 이때, power 메서드에 n이 아닌 n-1을 전달해야한다는 점을 주의해야합니다.
5. main 메서드
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
long n = Long.parseLong(br.readLine());
System.out.println(fibo(n));
}
구하려는 피보나치 수열을 입력 받고 출력하는 메서드입니다.
6. 분할 정복을 이용한 거듭제곱 방식의 시간 성능 테스트
아래는 long 타입의 최댓값인 900경번째 피보나치 수를 구할 때 걸리는 시간입니다.
5회 실행 결과
371μs
412μs
420μs
361μs
268μs
결과의 단위가 ms가 아닌 마이크로초(μs)라는 점에 주목할 필요가 있습니다. 1 ms는 1 μs의 1000배입니다.
각 방식별 시간 성능 비교
| 구분 | Recursion | DP with BigInteger | DP with Long | Power with Divide Conquer |
| n is | 40 | 100,000 | 10,000,000 | 9*10^19 |
| 1회차 | 231ms | 342ms | 49ms | 371μs |
| 2회차 | 341ms | 405ms | 32ms | 412μs |
| 3회차 | 232ms | 304ms | 41ms | 420μs |
| 4회차 | 278ms | 322ms | 41ms | 361μs |
| 5회차 | 221ms | 402ms | 38ms | 268μs |
| 평균 | 260.6ms | 355.0ms | 40.2ms | 366.4μs |
.
.
.
마치며
분할 정복을 이용한 거듭제곱 방식을 이해하는데 꽤 오랜 시간이 걸렸습니다. 저는 피보나치 기본 행렬이 왜 {1, 1, 1, 0}이 되어야하는지 이해가 안 돼서 한참을 헤맸던 것 같습니다. 하지만 피보나치 기본 행렬의 정의는 수학적 필연성이기 때문에 그냥 그렇구나..하고 받아들이면 됩니다.
이번 글에 수식이 많이 나와서 읽기 거북할 수 있지만 분할 정복을 이용한 거듭제곱을 이해하고 싶다면 꼭! 차근차근 이해하며 정독해보는 걸 추천드립니다.
글에서 분할 정복을 이용한 거듭제곱 개념까지 같이 설명했기 때문에 피보나치 수에서 확장해 더 다양한 문제도 풀 수 있을거라고 생각합니다.
이해가 안 되거나 궁금한 점 등은 댓글로 남겨주세요! 화이팅👍
'Algorithm' 카테고리의 다른 글
| [Algorithm] 그래프 이론 및 그래프 탐색 (0) | 2025.05.09 |
|---|---|
| [Algorithm] Floyd-Warshall 알고리즘 with JAVA (0) | 2025.04.26 |
| [Algorithm] Z 알고리즘 with JAVA (1) | 2025.02.21 |
| [Algorithm] CCW 알고리즘 with JAVA (1) | 2024.12.17 |
| [Algorithm] KMP 알고리즘 with JAVA (1) | 2024.12.10 |