들어가며
볼록 껍질을 구하는 그레이엄 스캔 알고리즘을 알기 위해선 CCW 알고리즘을 먼저 배워야합니다. CCW 알고리즘에 대해 자세히 설명해둔 글이 있으니 아래 링크 참고해주세요.
[Algorithm] CCW 알고리즘 with JAVA
들어가며최근에 기하와 관련된 문제를 풀며 점들이 이루는 방향성을 판별하는 알고리즘을 배우게 되었습니다. CCW 알고리즘은 세 점이 이루는 방향을 간단한 연산으로 확인할 수 있는 핵심 알고
jundyu.tistory.com
볼록 껍질: Convex Hull
1. 볼록한 다각형(Convex Polygon)

왼쪽 도형을 바깥에서 바라봤을 때 기준으로 모든 꼭짓점들이 볼록합니다. 하지만 오른쪽 도형은 빨간색으로 표시된 하나의 꼭짓점이 오목한 것을 볼 수 있습니다. 이렇게 모든 꼭짓점들이 볼록한 경우 볼록 다각형이라고 부르고, 정의는 아래와 같습니다.
볼록 다각형
1. 모든 내각의 크기가 180도 미만인 다각형
2. 또는, 다각형 내부의 두 점을 잇는 선분이 항상 다각형의 내부나 경계에만 포함되는 단순 다각형
2. 볼록 껍질(Convex hull)
그러면 볼록 껍질이 무엇인지 알아보겠습니다. 우선 아래와 같이 2차원 격자 위에 많은 점(Point)들이 놓여져있습니다.

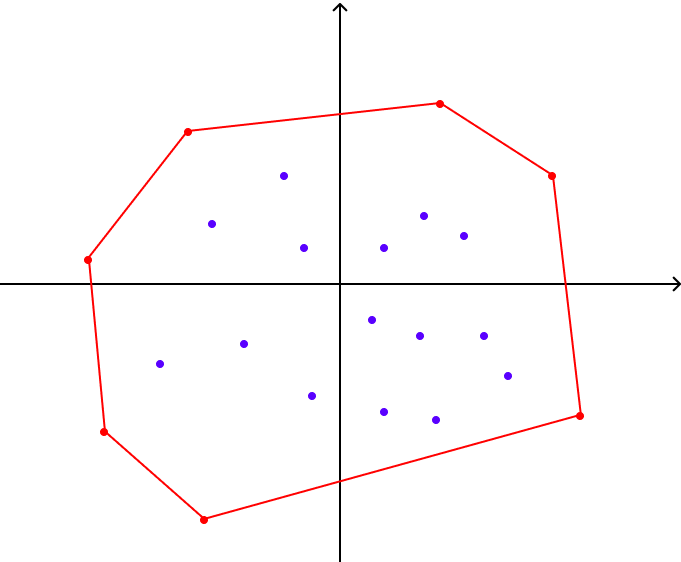
이 점들을 모두 포함하는 가장 작은 볼록 다각형을 오른쪽과 같이 그릴 수 있는데 이게 바로 볼록 껍질입니다. 쉽게 생각하면 바닥에 말뚝을 위의 좌표처럼 꽂아두고, 고무줄을 씌우면 위와 같은 볼록 껍질이 생깁니다. 볼록 껍질의 정의는 아래와 같습니다.
볼록 껍질
1. 주어짐 점들의 집합을 포함하는 가장 작은 볼록 다각형
2. 즉, 점들을 감싸는 가장 작은 볼록 다각형
볼록 껍질을 이해했다면 이제 본론으로 들어가보겠습니다. 이번 글에서 다룰 내용은 볼록 껍질을 구하는 그레이엄 스캔(Graham Scan) 알고리즘입니다. 볼록 껍질을 구하는 알고리즘으로 Andrew's Monotone Chain 알고리즘도 있지만 PS에서 더 많이 사용되는 Graham Scan 알고리즘만 다뤄보도록 하겠습니다.
Graham Scan Algorithm
1. 개요
Ronald Graham이 1972년에 고안해낸 블록 껍질을 구하는 대표적인 알고리즘입니다.
2. 동작 원리
- 좌표평면의 모든 점들을 기준점을 기준으로 각도 정렬합니다.
- 정렬한 점들을 하나씩 만날때마다 최근에 만났던 2개의 점까지 참고해서 3개의 점에 대해 볼록한지, 오목한지를 확인합니다. 이때 CCW 알고리즘이 활용됩니다.
- 각도 정렬을 했다면 각 점들을 반시계 방향으로 순회하게 됩니다.
- 이때, 반시계 방향이라면 스택에 push하고, 시계 방향이라면 스택의 TOP을 pop하며 전체를 순회합니다.
- 최종적으로 스택에 들어있는 점들이 볼록 껍질을 구성하는 집합입니다.
3. 시간 복잡도
시간복잡도는 O(n log n)입니다. 각도 n개의 점을 정렬하는데 O(n log n)이 걸리고, 기준점을 찾는 복잡도는 O(n), 스택을 활용하는 복잡도도 O(n)이므로 전체 시간복잡도는 O(n log n)이 됩니다.
기준점과 각도 정렬 방법
여기선 기준점을 정하는 방법과 각도 정렬 기준만 설명하고, 근거는 뒤에서 설명하겠습니다.
1. 기준점
기준점은 각도를 정렬하기 전에 정렬의 기준이 될 점입니다.
- y좌표가 가장 작은 점으로 선택합니다.
- 만약 y좌표가 같은 경우 x좌표가 가장 작은 점을 선택합니다.
2. 각도 정렬
각도 정렬이란 기준점을 영점으로 뒀을 때, 기준점에서 다른 점들로 향하는 벡터가 만들어내는 극각 순서대로 점들을 정렬하는 것을 말합니다.
- 각 점 $Q(x, y)$에 대해, 기준점 $P(x_0, y_0)$에서 벡터 $(x-x_0, y-y_0)$를 구합니다.
- 이 벡터가 x축과 이루는 각도를 기준으로 오름차순 정렬합니다.
- 이때의 각도는 $\tan^{-1}(\frac{y-y_0}{x-x_0})$에 해당됩니다.
- 만약 같은 각도를 가지는 점들이 있으면, 기준점에서 더 먼 점을 앞에 정렬합니다.
글로는 이해가 어려우니 바로 그림으로 동작을 따라가보겠습니다.
그림으로 이해하는 Graham Scan Algorithm
알고리즘 동작 과정의 이해를 돕기 위해 쉬운 예제를 만들어봤습니다. 숫자나 수식을 최대한 빼고 그림과 글로만 설명해보겠습니다.
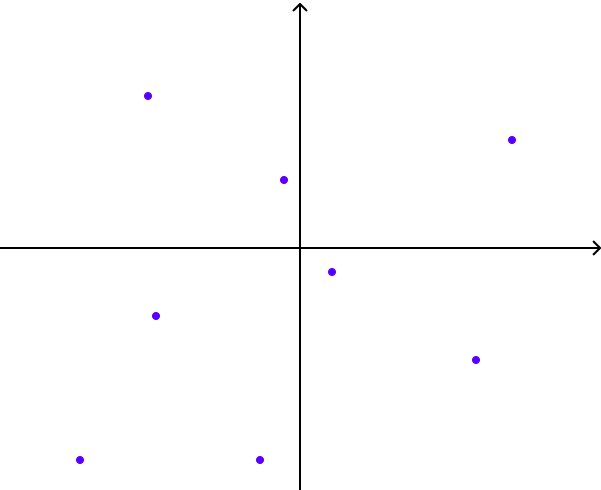
1. 기준점 정하기

위의 점에서 기준점은 가장 아래에 있고, 가장 왼쪽에 있는 빨간색 점에 해당합니다. 기준점을 $P(x_0, y_0)$으로 두겠습니다.
2. 각도 정렬하기
기준점을 영점이라고 생각하고 영점과 각 점 $Q(x-x_0, y-y_0)$들을 이으면 벡터가 생기고 이 벡터가 x축과 이루는 각은 $\tan{\theta}=\frac{y-y_0}{x-x_0}$입니다. 따라서 $\theta = \tan^{-1}\frac{y-y_0}{x-x_0}$입니다.
이 $\theta$의 크기를 오름차순으로 정렬하면 아래에 인덱싱(Indexing)한 순서와 같습니다.

여기서 3번과 4번점은 $\theta$의 크기가 동일하지만 3번 점이 4번 점보다 더 멀리 떨어져 있어서 3번 점을 앞에 배치했습니다.
3. 기준점과 1번 점을 스택에 push

기준점과 첫번째 점은 항상 최종 볼록 껍질에 포함됩니다. 단, $\theta$가 동일할 때 더 멀리 떨어진 점을 우선 정렬했다는 조건이 필요합니다.
4. 2번점과 스택의 점 2개에 대해 볼록 확인
이제 본격적으로 CCW를 이용해서 회전 방향을 판정해보겠습니다.

기준점, 1번점, 2번점 차례대로 따라가보면 반시계 방향으로 회전합니다. 볼록 다각형의 조건을 만족하므로 2번점을 스택에 넣습니다.

5. 3번점과 점 2개에 대해 볼록 확인

1, 2, 3번점의 회전 방향이 반시계 방향이므로 마찬가지로 3번점도 스택에 넣습니다.

6. 4번점과 점 2개에 대해 볼록 확인

2, 3, 4번점도 마찬가지로 반시계 방향으로 회전합니다. 따라서 4번 점도 스택에 넣습니다.

7. 5번점과 점 2개에 대해 볼록 확인

위의 그림을 보면 3, 4, 5번점들이 시계 방향으로 회전하고 있습니다. 따라서 4번점은 볼록 껍질에 해당하지 않는 점이고, 스택에서 pop해줍니다.

4번점을 pop하고 다시 스택에 남은 2, 3, 5번점으로 회전 방향을 확인해보니 반시계 방향입니다. 그러면 앞서 계속 했던 것처럼 스택에 5번점을 push합니다.

8. 6번점과 점 2개에 대해 볼록 확인

3, 5, 6번점이 반시계 방향으로 회전하고 있습니다. 스택에 6번점을 push합니다.

9. 7번점과 2개의 점에 대해 볼록 확인

5, 6, 7번점들이 시계 방향으로 회전하기 때문에 스택의 TOP에 위치한 점을 pop합니다.

6번점을 pop하고 다시 회전 방향을 확인해보니 또 시계 방향으로 회전하고 있습니다. 따라서 5번점도 볼록 껍질에 해당되지 않으므로 스택에서 pop합니다.

다시 2, 3, 7번점으로 회전 방향을 확인해보니 반시계 방향으로 회전합니다. 따라서 7번점을 스택에 push합니다.

10. 모든 점들을 순회 완료

모든 점들에 대해 볼록한 다각형을 이루는지 확인하며 순회했습니다. 이렇게 스택에 남아있는 $(P, 1, 2, 3, 7)$번점들이 볼록 껍질을 이루는 점이 된다는 것을 알 수 있습니다.
위의 동작 과정을 따라오면서 의문점이 여러가지 생겼을텐데 아래에서 모두 다뤄보겠습니다.
기준점과 각도 정렬
앞서 설명하겠다고 했던 기준점과 각도 정렬. 그리고 추가적으로 궁금할만한 점, 오해할만한 부분들에 대해 짚고 넘어가겠습니다.
1. 기준점이 가장 아래 점 중 가장 왼쪽 점인 이유
우선 기준점을 아래의 기준으로 가장 외곽에 둔다면 볼록 껍질의 출발점을 확정할 수 있습니다.
- 가장 아래에 있는 점 중에, 가장 왼쪽에 있는 점
- 가장 아래에 있는 점 중에, 가장 오른쪽에 있는 점
- 가장 위에 있는 점 중에, 가장 왼쪽에 있는 점
- 가장 위에 있는 점 중에, 가장 오른쪽에 있는 점
그리고 네가지의 출발점 중 어느 점을 기준으로 삼아도 출발점으로 쓸 수 있지만, 가장 아래에 있고, 가장 왼쪽에 있는 점을 선택하면 몇 가지의 장점이 있습니다.
- $\tan^{-1}$ 함수의 형태로 각 벡터들의 $\theta$를 구하기가 쉬워집니다.
- 기준점을 기준으로 반시계 방향으로 스캔할 때 최대 180˚ 이내의 점들만 고려하면 되므로 각도를 정렬하기 훨씬 간단해지고, 직관적입니다.
2. 각도 정렬이 필요한 이유
각 점들이 기준점과 만들어낸 벡터를 x축과의 각을 기준으로 오름차순 정렬하는 이유는 볼록 껍질을 한 바퀴 돌면서 외곽의 점들을 차례로 방문하기 위해서입니다.
또한, 각 $\theta$가 동일할 때는 거리가 먼 점부터 정렬합니다. 그 이유는 같은 직선 위에 점들이 놓여있을 때 기준점에서 가장 멀리 떨어진 점만이 껍질의 외곽을 형성하기 때문입니다. 따라서 정렬 시 멀리 있는 점부터 우선 배치하거나, 멀리 있는 점 하나만 남겨둔다면 스택 처리 과정에서 불필요한 연산이 줄어듭니다.
3. $\tan^{-1}$을 쓰지 않고 정렬하는 방법
외적(cross product)을 이용하면 역삼각함수를 사용하지 않고도 정렬이 가능합니다. 구현 자체는 역삼각함수를 사용하는 것이 더 쉽기 때문에 자세한 설명은 생략하겠습니다.
4. 스택에 기준점을 넣는 이유
처음 알고리즘 동작을 설명할 때 스택에 미리 기준점과 1번점을 넣어놓고 스캔을 시작했습니다. 하지만 이건 구현하는 방식의 차이일뿐 기준점이나 1번점을 넣지 않고 시작하는 것도 상관없습니다.
아래 구현 코드에서 스택에 미리 점을 넣지 않고 스캔하는 방식을 설명하겠습니다.
Graham Scan Algorithm 실제 코드로 구현하기
1. Point Class
public static class Point implements Comparable<Point> {
long x, y;
double angle;
public Point(long x, long y) {
this.x = x;
this.y = y;
}
private static long getDist(Point a, Point b) {
return (a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y);
}
@Override
public int compareTo(Point o) {
if(this.angle == o.angle) return Long.compare(getDist(standard, this), getDist(standard, o));
return Double.compare(this.angle, o.angle);
}
}Point 자료구조를 만들어서 각 점의 x, y 좌표쌍과 기준점과 이루는 각 angle을 저장합니다.
- angle은 double 자료형으로 저장해야합니다.
- Comparable 인터페이스를 구현해서 Point 자료구조의 정렬 기준인 compareTo를 설정합니다.
- 앞서 설명했듯이 기준점과 만들어낸 선분의 각 $\theta$를 기준으로 오름차순 정렬합니다.
- 만약 각이 동일하다면 getDist 함수로 거리가 먼 점부터 정렬합니다.
2. CCW Method
public static int ccw(Point a, Point b, Point c) {
long calc = (b.x - a.x)*(c.y - a.y) - (b.y - a.y)*(c.x - a.x);
if(calc > 0) return 1;
else if(calc < 0) return -1;
else return 0;
}
벡터의 외적으로 회전 방향을 판별해주는 메서드 ccw를 구현했습니다.
- 외적값이 양수면 1을 반환해서 반시계 방향으로 회전함을 반환
- 외적값이 음수면 -1을 반환해서 시계 방향으로 회전함을 반환
- 외적값이 0이면 0을 반환해서 직선임을 반환
3. Main Logic
메인 흐름은 코드 내에 주석으로 설명하겠습니다.
public class Convex_Hull {
// 기준점으로 사용할 standard 변수
static Point standard;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 점의 개수
int n = Integer.parseInt(br.readLine());
// 각 점을 저장할 컬렉션 프레임워크
List<Point> point = new ArrayList<>();
StringTokenizer st;
for(int i = 0; i < n; i++) {
st = new StringTokenizer(br.readLine(), " ");
// 아직 기준점을 정하지 않았으므로 angle도 알 수 없음
// Point는 우선 좌표만 저장
point.add(new Point(Long.parseLong(st.nextToken()), Long.parseLong(st.nextToken())));
}
// 기준점 선택
// y가 가장 작고, 그 중에 x가 가장 작은 점으로 선택
standard = Collections.min(point, (a, b) -> {
if (a.y != b.y) return Long.compare(a.y, b.y);
return Long.compare(a.x, b.x);
});
// 기준점은 순회할 필요 없으므로 List에서 제거
point.remove(standard);
// 각 점들에 대해 angle 계산
for(Point out : point) {
out.angle = Math.atan2(out.y-standard.y, out.x-standard.x);
}
// 정렬
Collections.sort(point);
// 스택 로직
Stack<Point> stack = new Stack<>();
for(Point out : point) {
// stack.size() >= 2 :
while(stack.size() >= 2 && ccw(stack.get(stack.size() - 2), stack.peek(), out) <= 0) {
stack.pop();
}
stack.push(out);
}
System.out.println(stack.size());
}
public static int ccw(Point a, Point b, Point c) {}
public static class Point implements Comparable<Point> {}
}
4. Stack Logic
Stack<Point> stack = new Stack<>();
for(Point out : point) {
while(stack.size() >= 2 && ccw(stack.get(stack.size() - 2), stack.peek(), out) <= 0) {
stack.pop();
}
stack.push(out);
}- stack.size() >= 2 : 현재 만난 out점과 스택에 들어있는 상위 2개의 점으로 CCW를 호출해야하는데 스택에 1개 이하의 점만 존재하는 경우 불가능
- ccw(stack.get(stack.size()-2), stack.peek(), out) <= 0 : 스택의 위에서 2번째 점, 첫번째 점, 현재 만난 점 out으로 ccw 확인
- while(condition) { stack.pop(); } : 오목한 부분을 만들기 때문에 스택의 첫번째 점 pop
- for(condition) { stack.push(out); } : 현재 점이 볼록한 각을 만들기 때문에 push
만약 문제의 요구사항에서 볼록 껍질의 직선 상에 있는 모든 점도 포함하라고 한다면 while문의 조건식에 등호를 빼면 됩니다.
전체 로직은 너무 길어서 생략했습니다. 위의 코드를 이해하고 조합해보면 코드가 나옵니다!
.
.
.
마치며
볼록 껍질과 그레이엄 스캔 알고리즘을 익히기 좋은 문제를 아래에 적어뒀습니다!
- 1708번 볼록 껍질 : https://www.acmicpc.net/problem/1708
- 2699번 격자점 컨벡스헐 : https://www.acmicpc.net/problem/2699
- 17403번 가장 높고 넓은 성 : https://www.acmicpc.net/problem/17403
위의 두 문제는 기본적인 Convex hull을 구하는 문제이지만 2699번은 기준점이 다르다는 것에 주의해야합니다. 마지막 문제는 Graham Scan을 간단히 응용해서 Convex hull을 겹겹이 구하는 문제입니다.
이상으로 볼록 껍질(Convex Hull)과 그레이엄 스캔(Graham Scan) 알고리즘에 대해 설명을 마치겠습니다!
궁금한 점이나 피드백은 댓글 환영합니다😊
'Algorithm > Geometry' 카테고리의 다른 글
| [Algorithm] 기하 알고리즘 해결을 위한 수학 공식 및 정리 모음 with Java (0) | 2026.01.17 |
|---|---|
| [Algorithm] CCW 알고리즘 with JAVA (1) | 2024.12.17 |