
들어가며
우리가 일상적으로 사용하는 수식은 대부분 중위 표기법(Infix Notation)입니다. 그러나 수식을 표현하는 방법에는 전위 표기법(Prefix Notation), 후위 표기법(Postfix Notation)도 존재합니다. 이번 글에서는 각각의 표기법에 대해 간단히 알아본 뒤 후위 표기법을 왜 사용해야하는 지와 중위 표기법을 후위 표기법으로 어떻게 변환하는 지에 대해 다뤄보겠습니다. 글의 마지막에 표기법끼리 변환하는 방법도 있으니 참고해주세요.
수식 표기법
우선 수식 표기법에 대해 간단히 알아보고 지나가겠습니다. 수식 표기법은 총 3가지로 분류됩니다.
- 전위 표기법 : Prefix Notaion(PN = Polish Notation)
- 중위 표기법 : Infix Notaion
- 후위 표기법 : Postfix Notaion(RPN = Reverse Polish Notation)
전위 표기법과 후위 표기법은 1924년 폴란드의 논리학자 얀 우카시에비치(Jan Lukasiewicz)가 명제 논리를 단순화하기 위해 고안했습니다. 폴란드 표기법(PN)이라는 이름은 언어권에 따라 우카시에비치 표기법, 바르샤바 표기법, 전위 표기법 등으로도 불립니다.
후위 표기법은 전위 표기법과는 반대의 성향을 가지므로 Reverse Polish Notation. 즉 RPN(Postfix Notaion)으로 불립니다.
그러면 이제 중위 표기법으로 표현된 아래의 예시 수식에 대해 전위 표기법과 후위 표기법이 어떻게 다른지 알아보겠습니다.
$$\huge A*(B+C)-D$$
1. 전위 표기법
$$\large -*A+BCD $$
연산자가 숫자의 앞쪽으로 치우친 것을 볼 수 있습니다. 전위 표기법은 연산자를 피연산자의 앞쪽에 배치하는 방법입니다. 예를 들어 $A+B$는 $+AB$가 됩니다.
2. 중위 표기법
$$\large A*(B+C)-D $$
우리가 흔히 수식을 표현하는 방식입니다.
3. 후위 표기법
$$\large ABC+*D- $$
연산자가 숫자의 뒤쪽으로 치우친 것을 볼 수 있습니다. 후위 표기법은 연산자를 피연산자의 뒤에 배치하는 방법입니다. 예를 들어 $A-B$는 $AB-$가 됩니다.
후위 표기법
본론으로 들어와서 후위 표기법 설명을 시작하겠습니다. 중위 표기법을 후위 표기법으로 어떻게 바꾸는 지와, 왜 후위 표기법이 중요한 지를 알아야합니다.
1. 후위 표기법을 사용하는 이유
$$\huge 3+4*2-5$$
사람은 위의 수식을 계산할 때 수식 전체를 보고 연산자의 우선순위에 따라 계산 순서를 각각 정한 뒤에 계산을 시작합니다. 사람은 한 눈에 $4*2$가 괄호 안에 있는 것을 볼 수 있어서 곱셈부터 계산할 수 있지만 컴퓨터는 어떨까요?
컴퓨터에 수식을 입력하면 컴퓨터는 왼쪽부터 차례대로 수식을 읽어들입니다. 컴퓨터는 사람처럼 수식 전체를 파악할 수 없기 때문에 처음 등장하는 $3+4$라는 피연산자(3과 4)와 연산자(+)를 읽어도 바로 계산할 수 없습니다. 뒤에 어떤 연산자가 등장하는 지 모르기 때문입니다.
따라서 컴퓨터는 스택이라는 자료구조를 이용해서 연산자의 우선순위에 따라 계산을 진행해야합니다. 스택을 사용해서 어떻게 후위 표기법으로 변환하는 지 보겠습니다.
2. Shunting Yard Algorithm과 후위 표기법
이번 글의 제목이 Shunting Yard Algorithm인데 드디어 설명할 시간이 됐습니다! 한국말로 번역하면 차량(또는 철도) 기지 알고리즘입니다. 이 차량 기지 알고리즘은 중위 표기법으로 표현된 수식을 후위 표기법으로 변환하는 알고리즘인데, 넓은 의미로는 토큰을 읽어서 우선순위와 결합법칙을 반영하여 재배치하는 알고리즘입니다. 최단 경로를 찾는 데이크스트라 알고리즘으로 유명한 에르허츠 데이크스트라가 1961년에 최초로 발표한 알고리즘입니다.
철도 기지라는 이름이 붙은 이유는 철도 기지에서 열차 칸을 임시로 세웠다가 다시 연결하듯, 연산자를 스택에 임시로 저장했다가 적절한 시점에 꺼내서 사용한다는 점에서 착안했기 때문입니다.
알고리즘의 개발 목적은 후위 표기법으로 변환하기 위함이었지만 더 확장해서 전위 표기법으로의 변환도 가능합니다. 하지만 이번 글에서는 차량 기지 알고리즘을 후위 표기법으로 변환해주는 알고리즘으로만 한정해서 보겠습니다.
3. 후위 표기법으로 변환하는 규칙
후위 표기법으로 변환할 때 미리 알고 가야하는 규칙들이 있습니다.
1. 피연산자는 그냥 출력
피연산자인 숫자는 단순히 계산 대상이므로 피연산자를 만나면 그대로 출력합니다.
2. 연산자 간의 우선순위를 고려
우선순위는 수식에서 먼저 계산됨을 의미하므로 아래와 같이 우선순위를 정할 수 있습니다.
| 우선순위 | 연산자 | |
| 1 | 거듭제곱 | ^ |
| 2 | 곱셈, 나눗셈 | *, / |
| 3 | 덧셈, 뺄셈 | +, - |
말보단 그림으로 이해하는 것이 훨씬 도움 될 것 같기 때문에 아래 글은 빠르게 읽고 넘어가겠습니다!
스택의 TOP에 위치한 연산자와 비교할 연산자가 만난 경우 만약 스택의 상단 연산자가 더 크면 스택의 연산자를 출력합니다. 이때, 여전히 스택에 연산자가 존재할 수 있는데 스택의 TOP 연산자보다 비교할 연산자의 우선순위가 작다면 계속 출력합니다. 그러다가 비교할 연산자의 우선순위가 더 커지는 순간이 오는데 그때 스택에 연산자를 push 해줍니다.
또한, 만약 같은 우선순위의 연산자를 비교하는 경우엔 스택에 먼저 들어갔던 연산자의 우선순위가 더 높다고 판정합니다.
괄호의 우선순위?
괄호는 연산자와는 별개로 처리해야합니다. 열린 괄호를 만나면 바로 push하고, 닫힌 괄호를 만나면 열린 괄호를 만날 때까지 모두 pop해서 출력합니다. 따라서 우선순위는 최하위로 둬야합니다.
3. 괄호
당연하게도 올바른 수식이 입력될 때 열린 괄호가 존재하면 이후에 닫힌 괄호도 반드시 하나 입력됩니다. 후위 표기식으로 표현할 땐 괄호는 출력하지 않습니다.
4. 후위 표기법으로 변환(Shunting Yard Algorithm 동작)

위와 같이 오른쪽의 중위 표기법으로 수식이 주어진 경우를 예로 들어 설명을 시작하겠습니다.
i) 3은 피연산자이므로 바로 출력

3은 피연산자이므로 앞서 설명한 규칙에 따라 바로 출력하면 됩니다. 따라서 왼쪽 후위 표기식의 처음 위치에 자리잡게 됩니다.
ii) +는 연산자이므로 스택에 넣는 것을 고려

+는 연산자입니다. 연산자가 나타난 경우 이미 스택에 존재하는 연산자와 우선순위를 비교해야합니다. 하지만 위처럼 스택이 비어있는 경우는 반드시 스택에 삽입합니다.
스택이 비어있을 때 비교없이 push를 하는 이유가 뭘까?
스택이 비어있다는 것은 비교할 대상이 없다는 것을 의미합니다. 따라서 우선순위 충돌 위험이 없기 때문에 새로 만난 연산자는 그대로 스택에 push하면 됩니다. 이렇게 스택에 넣어둬야 이후에 등장하는 연산자와 우선순위를 비교하거나, 마지막에 스택에서 꺼내 출력할 수 있습니다.
따라서 아래와 같이 스택에 + 연산자가 들어가게 됩니다.

iii) 4는 피연산자이므로 바로 출력

숫자 4 역시 피연산자이므로 바로 출력하면 됩니다.
iv) *는 연산자이므로 스택에 넣는 것을 고려

피연산자인 곱셈을 만났습니다. 곱셈의 우선순위는 덧셈보다 더 크기 때문에 알고리즘 규칙에 따라 스택에 push 해줍니다.
그러면 아래와 같이 바뀝니다.

v) 2는 피연산자이므로 바로 출력

숫자 2는 피연산자입니다. 마찬가지로 바로 출력해줍니다.
vi) 마이너스(-)는 연산자이므로 스택에 넣는 것을 고려

마이너스 연산자가 나타났습니다. 마이너스 연산자를 스택의 TOP 연산자와 비교해보면 마이너스 연산자의 우선순위가 더 낮은 것을 알 수 있습니다. 따라서 스택에 들어있는 곱셈 연산자를 꺼내서 출력합니다.

그럼 이제 다시 마이너스 연산자와 스택의 TOP 연산자를 비교해봅니다. +와 -의 연산자는 우선순위가 같지만 우선순위가 같아도 먼저 스택에 들어갔던 연산자의 우선순위가 더 높기 때문에 덧셈 연산자를 꺼내서 출력합니다.

마지막으로 스택은 비어있게 되므로 마이너스 연산자는 아래와 같이 스택에 삽입됩니다.

vii) 5는 피연산자이므로 그대로 출력

마지막 피연산자 5까지 출력해줍니다. 그러면 이로써 기본적인 연산은 모두 끝났습니다.
하지만 수식의 길이만큼 위의 과정을 거쳤어도 스택에는 반드시 하나 이상의 연산자가 남습니다. 따라서 스택에 남아있는 연산자까지 출력해야 최종적인 후위 표기식이 완성됩니다.
vii) 스택에 남은 연산자 모두 출력

스택에 남아있던 마이너스 연산자까지 출력하면 비로소 후위 표기식이 완성됩니다.
만약 수식에 괄호가 포함된 경우 닫는 괄호가 나오는 즉시 스택 내에 모든 연산자를 출력해줘야합니다. 괄호 내의 수식은 하나의 연산 그룹을 의미하기 때문입니다. 괄호가 포함된 수식에 대한 흐름을 보고 싶다면 아래를 참고해주세요.

위의 수식에 대해 중요한 부분만 주석으로 설명했습니다. 그림을 클릭하면 더 자세히 볼 수 있습니다.

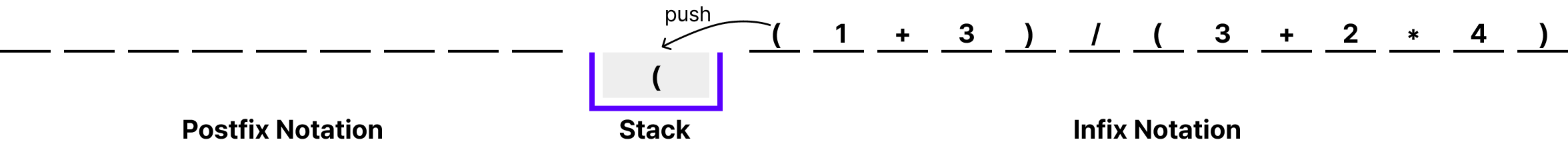












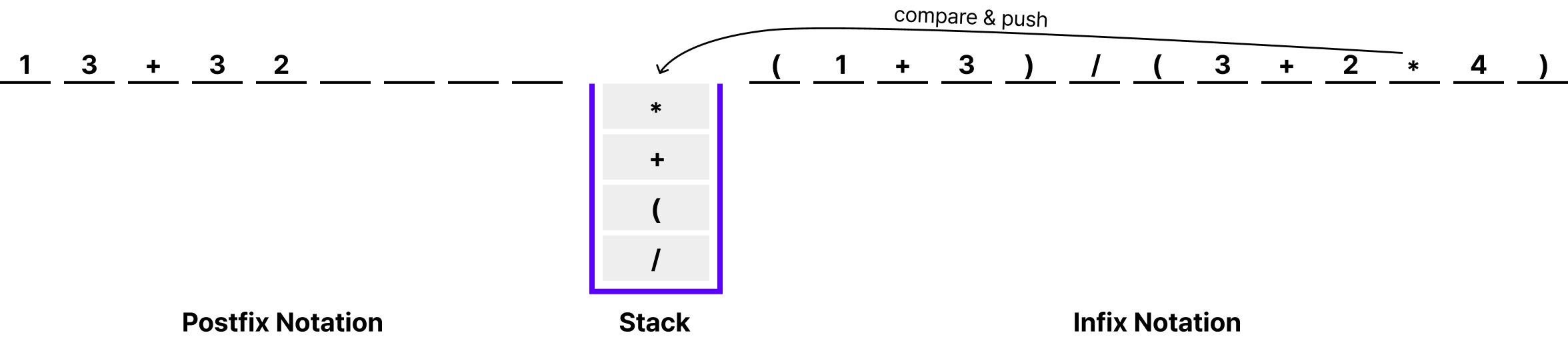







지금까지 중위 표기법으로 표현된 수식을 후위 표기법으로 변환하는 과정을 그림으로 이해했습니다. 다음 장에선 실제 자바 코드로 Shunting Yard 알고리즘을 구현하는 내용을 다뤄보겠습니다.
Shunting Yard Algorithm 자바 코드로 구현
아래의 코드가 차량 기지 알고리즘의 일반적인 틀(Frame)입니다. 원활한 설명을 위해 코드 내 주석으로 설명을 진행하겠습니다.
// import 생략
public class Shunting_Yard_Algorithm {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 수식을 char 배열로 입력
char[] exp = br.readLine().toCharArray();
// 차량 기지 역할을 하는 스택
Stack<Character> stack = new Stack<>();
// 출력을 위한 버퍼
StringBuilder sb = new StringBuilder();
for (int i = 0; i < exp.length; i++) { // 수식의 0부터 접근
// 현재 다룰 수식의 연산자 또는 피연산자 c
char c = exp[i];
if (c >= '0' && c <= '9') { // 피연산자인지 확인
// 피연산자는 바로 출력
sb.append(c);
} else if (c == '(') { // 열린 괄호인지 체크
// 열린 괄호는 우선순위 비교없이 바로 스택에 push
stack.push(c);
} else if (c == ')') { // 닫힌 괄호인지 체크
// 닫힌 괄호는 열린 괄호가 나올 때까지
// 스택 내의 모든 연산자 출력
while (!stack.isEmpty() && stack.peek() != '(') {
sb.append(stack.pop());
}
// 스택 내에 있던 열린 괄호는 pop해서 버림
stack.pop();
} else { // 연산자인 경우
// 스택에 연산자가 존재하는 경우에 우선순위를 비교
while (!stack.isEmpty() && priority(stack.peek()) >= priority(c)) {
// 스택의 top 연산자의 우선순위가 새로운 연산자보다
// 우선순위가 높으면 아닐때까지 계속 출력
sb.append(stack.pop());
}
// 그러고 새로운 연산자인 c push
stack.push(c);
}
}
// 스택에 남아있던 최소 한 개의 연산자 모두 출력
while (!stack.isEmpty()) {
sb.append(stack.pop());
}
System.out.println(sb.toString().trim());
}
// 우선순위 비교 메서드로
// 숫자가 높을수록 우선순위가 높음
private static int priority(char op) {
if (op == '(') return 0;
if (op == '+' || op == '-') return 1;
if (op == '*' || op == '/') return 2;
return -1;
}
}
후위 표기법의 계산
그러면 후위 표기법으로 수식이 주어진 경우 어떻게 계산할 수 있을까요? 마찬가지로 스택을 사용하지만 규칙이 살짝 다릅니다.
1. 후위 표기법 계산 규칙
- 피연산자가 나오면 바로 스택에 삽입
- 연산자가 나오면 스택에서 2개의 피연산자를 pop해서 연산 수행 후 결과값을 다시 push
- 연산 방향은 항상 $pop_2\ \begin{smallmatrix} +-\\\times\div \end{smallmatrix}\ pop_1$
- 괄호는 없으므로 고려하지 않음
- 우선순위도 고려할 필요 없음
2. 후위 표기법 계산 과정
앞서 후위 표기식으로 만들었던 예제인 $3+4*2-5$ 수식을 스택을 이용해 계산해보겠습니다.

i) 3은 피연산자이므로 스택에 삽입

앞선 규칙에 따라 피연산자는 바로 스택에 삽입합니다.
ii) 4는 피연산자이므로 스택에 삽입

앞선 규칙에 따라 피연산자인 4역시 바로 스택에 삽입합니다.
iii) 2는 피연산자이므로 스택에 삽입

앞선 규칙에 따라 피연산자인 2까지 바로 스택에 삽입합니다.
iv) 연산자를 만나면 계산 실행

연산자를 만나면 스택 top의 두 피연산자를 꺼내서 계산을 실행하면 됩니다. 4와 2를 곱하면 8이 되고, 중간값 8을 아래처럼 다시 스택에 넣어줍니다.

v) 연산자를 만나면 계산 실행

마찬가지로 덧셈 연산자를 만났으므로 8과 3을 pop해서 덧셈을 진행한 뒤 아래처럼 11을 push합니다.

vi) 5는 피연산자이므로 스택에 삽입

5는 피연산자니까 스택에 삽입했습니다.
vi) 연산자를 만나면 계산 실행

연산자 마이너스를 만났습니다. 곱셈이나 덧셈은 피연산자의 순서가 상관없었지만 뺄셈이나 나눗셈은 순서가 중요합니다. 스택의 더 깊은 곳에 위치한다는 것은 수식상 순서가 앞선다는 뜻이므로 11에서 5를 빼야합니다.
계산 결과인 6을 아래처럼 다시 스택에 push 합니다.

vii) 후위 표기식 순회가 끝나면 스택에 남은 값이 결과값

이렇게 후위 표기식으로 표현된 수식을 모두 순회하고 스택에 마지막으로 남은 값이 수식의 결과값이 됩니다.
3. 후위 표기법 계산 코드
아래는 후위 표기법으로 표현된 수식 계산을 코드로 구현한 것입니다.
// import 생략
public class Postfix_Notation_Calculator {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 수식 입력
char[] input = br.readLine().toCharArray();
// 피연산자를 담아둘 차량 기지
Stack<Double> stack = new Stack<>();
for(int i = 0; i < input.length; i++) {
switch(input[i]) {
case '+' : {
stack.push(stack.pop()+stack.pop());
break;
}
case '-' : {
double a = stack.pop();
double b = stack.pop();
stack.push(b-a);
break;
}
case '*' : {
stack.push(stack.pop()*stack.pop());
break;
}
case '/' : {
double a = stack.pop();
double b = stack.pop();
stack.push(b/a);
break;
}
default : { // 피연산자인 경우 바로 스택에 삽입
stack.push((double) (input[i]-'0'));
}
}
}
System.out.printf("%.2f", stack.pop());
}
}
수식 표기법끼리 변환
앞서 중위 표기법에서 후위 표기법으로 변환하는 방법은 자세히 알아보았습니다. 하지만 일반적으로 표기법은 3가지가 있고 각각 변환하는 방법은 ${}_{3}P_{2}=6$ 가지가 존재합니다. 나머지 5가지 방법도 간단하게 메서드로만 확인하고 넘어가겠습니다.
1. 후위 표기법에서 중위 표기법으로 전환
static String PostfixToInfix(char[] exp) {
Stack<String> st = new Stack<>();
for(char c : exp) {
if(c == '+' || c == '-' || c == '*' || c == '/') {
String right = st.pop();
String left = st.pop();
st.push("(" + left + c + right + ")");
} else {
st.push(String.valueOf(c));
}
}
return st.pop();
}
2. 중위 표기법에서 전위 표기법으로 변환
static String InfixToPrefix(char[] exp) {
Stack<Character> ops = newStack<>();
Stack<String> vals = new Stack<>();
for(char c : exp) {
if(Character.isLetterOrDigit(c)) { // 피연산자 삽입
vals.push(String.valueOf(c));
} else if(c=='(') { // 열린 괄호
ops.push(c);
} else if(c==')') { // 닫힌 괄호
while(!ops.isEmpty() && ops.peek()!='(') {
char op = ops.pop();
String r = vals.pop()
String l = vals.pop();
vals.push(op + l + r);
}
ops.pop(); // 열린 괄호 제거
} else if(c == '+' || c == '-' || c == '*' || c == '/') { // 연산자인 경우
while(!ops.isEmpty() && ops.peek() != '(' && prec(ops.peek()) >= prec(c)){
char op = ops.pop();
String r = vals.pop()
String l = vals.pop();
vals.push(op + l + r);
}
ops.push(c);
}
}
while(!ops.isEmpty()){
char op = ops.pop();
String r = vals.pop(), l = vals.pop();
vals.push(op + l + r);
}
return vals.pop();
}
3. 전위 표기법에서 중위 표기법으로 전환
static String PrefixToInfix(char[] exp){
Stack<String> st = new Stack<>();
for(int i = exp.length - 1; i >= 0; i--){
char c = exp[i];
if(c == '+' || c == '-' || c == '*' || c == '/'){
String left = st.pop(), right = st.pop();
st.push("(" + left + c + right + ")");
} else {
st.push(String.valueOf(c));
}
}
return st.pop();
}
4. 전위 표기법에서 후위 표기법으로 변환
static String PrefixToPostfix(char[] exp){
Stack<String> st = new Stack<>();
for(int i = exp.length - 1; i >= 0; i--){
char c = exp[i];
if(c == '+' || c == '-' || c == '*' || c == '/'){
String left = st.pop(), right = st.pop();
st.push(left + right + c);
} else {
st.push(String.valueOf(c));
}
}
return st.pop();
}
5. 후위 표기법에서 전위 표기법으로 전환
static String PostfixToPrefix(char[] exp){
Stack<String> st = new Stack<>();
for(char c: exp) {
if(c == '+' || c == '-' || c == '*' || c == '/'){
String right = st.pop(), left = st.pop();
st.push(c + left + right);
} else {
st.push(String.valueOf(c));
}
}
return st.pop();
}
.
.
.
마치며
백준에 후위 표기법을 연습하기 좋은 문제가 몇가지 있으니 추천하고 마무리 짓겠습니다. 문제는 난이도 오름차순으로 배치했습니다.
- 1935번 후위 표기식2 : https://www.acmicpc.net/problem/1935
- 6828번 From Prefix to Postfix : https://www.acmicpc.net/problem/6828
- 1918번 후위 표기식 : https://www.acmicpc.net/problem/1918
처음과 끝의 문제는 문제명에서 알 수 있듯이 후위 표기식과 중위 표기식 간의 변환을 다루고, 중간의 문제는 전위 표기식과 후위 표기식 간의 문제를 다룹니다.
후위 표기법과 션팅 야드 알고리즘은 간단히 요약할 수도 있지만, 그렇게 하면 다른 글들과 크게 다르지 않았을 것 같습니다. 그래서 원리와 과정을 최대한 자세히 풀어 쓰다 보니 글이 조금 길어졌네요. 이 글이 후위 표기법을 더 깊이 이해하는 데 도움이 되었길 바랍니다.
긴 글 읽어주셔서 감사합니다. 피드백이나 질문 환영합니다! 😊
'Algorithm' 카테고리의 다른 글
| [Algorithm] 누적합(Prefix Sum) 알고리즘 with Java (5) | 2025.08.07 |
|---|---|
| [Algorithm] 분할 정복을 이용한 행렬의 거듭제곱으로 Fibonacci 수열 구하기 with JAVA (0) | 2025.01.07 |